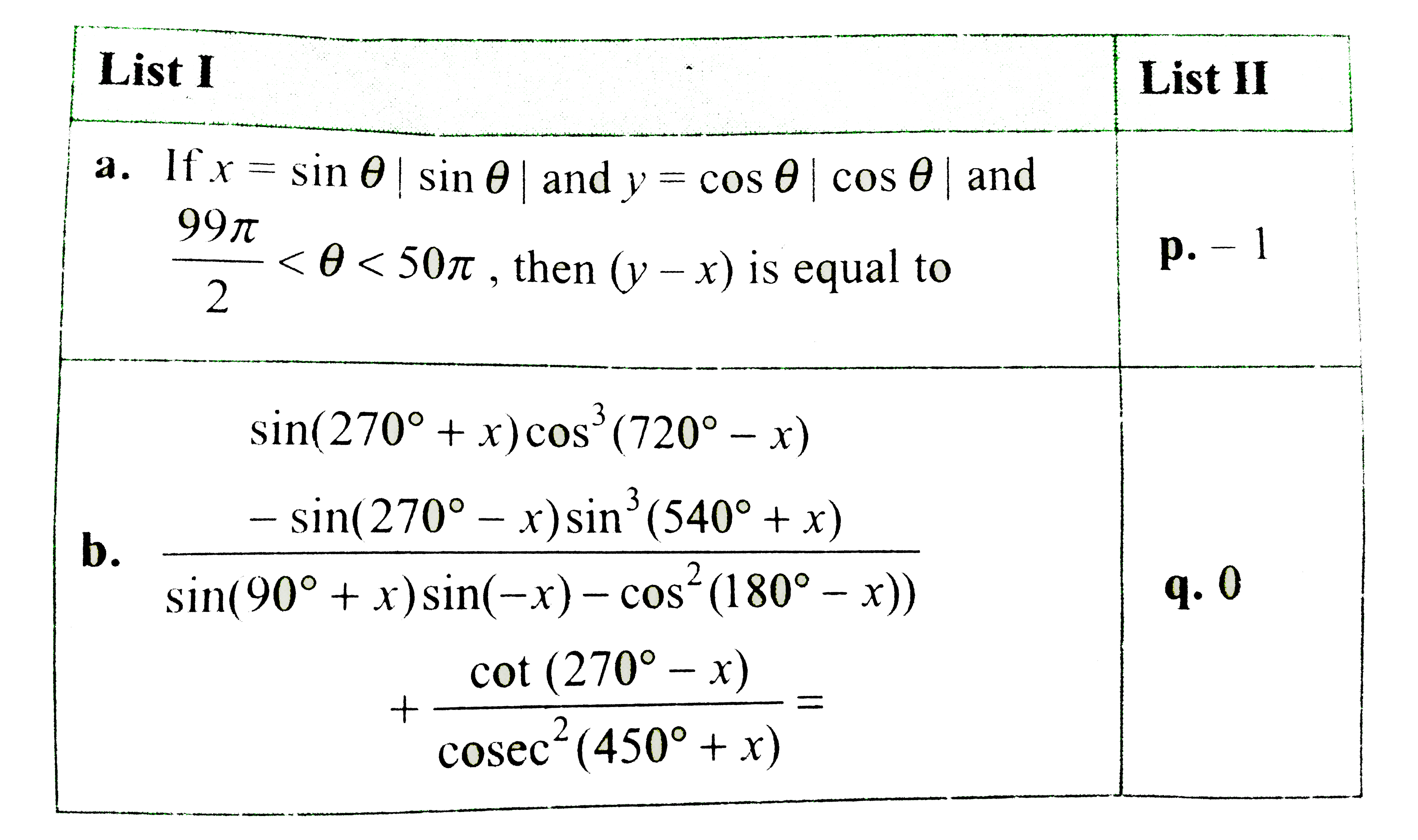
In $DeltaA B C, B C = 1, \frac{sin A}{2} = x_{1}, \frac{sin B}{2} = x_{2} \frac{cos A}{2} = x_{3}$ and $\frac{cos B}{2} = x_{4} w i t h {(x ? \frac{1}{x_{2}})}^{2007} - {(\frac{x_{3}}{x_{4}})}^{2006} = 0$ Length of side AC is equal to: 1/2 (b) 1 (c) 2 (d) cant be determined If $∠ A = 90^{0}, t h e n a r e a o f A B C$ is 1/2 sq. units (b) 1/3 sq. units 1 sq.. units (d) 2 sq. unitsSolution in Tamil

A

$\frac{1}{2}$

B

1

C

2

D

can't be determined

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

In given $Δ A B C both \frac{A}{2} and \frac{B}{2} lie strictly in (0, \frac{π}{2}) and sin x always increasing in (0, \frac{π}{2})$ whereas cos x is always decreasing in $(0, \frac{π}{2})$ .
So, if $\frac{A}{2} < \frac{B}{2}$
$\Rightarrow \frac{sin (A)}{2} > \frac{sin (B)}{2}$
$or x_{1} > x_{2}$
$and x_{3} < x_{4}$
$or \frac{1}{x^{3}} > \frac{1}{x^{4}}$
So, $x_{1}^{2007} x_{4}^{2006} = x_{2}^{2007} x_{3}^{2006}$ is not valid.
Similarly for $\frac{A}{2} < \frac{B}{2}$
$\Rightarrow \frac{sin (A)}{2} \frac{sin (B)}{2}$
$\Rightarrow x_{1} < x_{2}$
$and \frac{1}{x^{3}} < \frac{1}{x^{4}}$
For this also $x_{1}^{2007} x_{4}^{2006} = x_{2}^{2007} x_{3}^{2006}$ is not valid.
So, ${(\frac{x_{1}}{x_{2}})}^{2007} - {(\frac{x_{3}}{x_{4}})}^{2006} = 0 is possible only when \frac{A}{2} = \frac{B}{2}$ .
$\Rightarrow x_{1} = x_{2} and \frac{1}{x_{3}} = \frac{1}{x_{4}}$
Hence, $Δ A B C$ is isosceles with $∠ A B C = ∠ C A B$ .
$\Rightarrow B C = A C = 1 unit$
if $∠ A = 90^{\circ}$
Area, $A = \frac{1}{2} B C \times A C = \frac{1}{2} sq. units$

|

Updated on:21/07/2023

Class 12 MATHS TRIGONOMETRIC FUNCTIONS

Topper's Solved these Questions

Similar Questions

CENGAGE-TRIGONOMETRIC FUNCTIONS -Exercise (Comprehension)

Home
Ask Doubt
Profile