Question

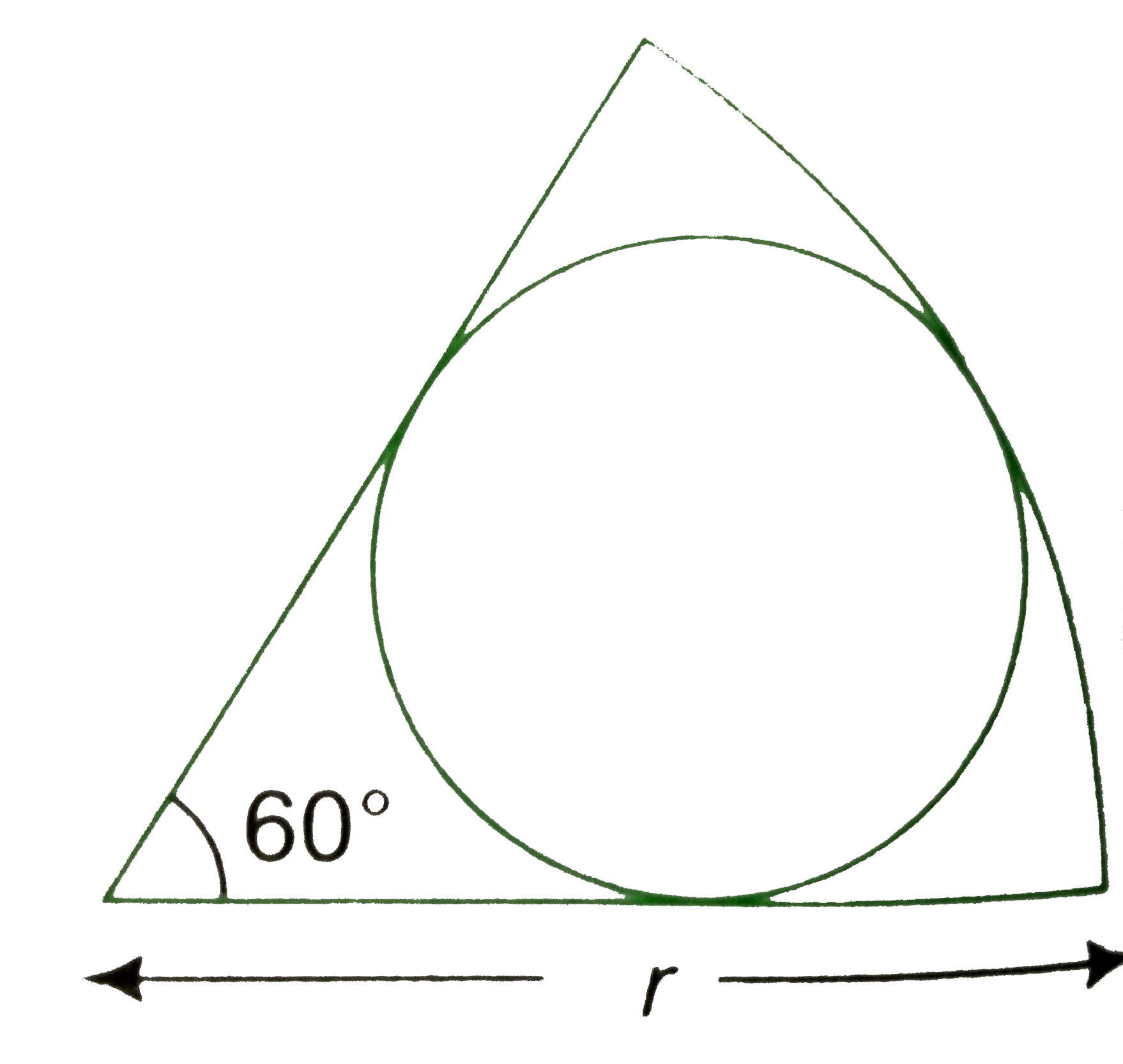
A circle is drawn in a sector of a larger circle of radius $r,$
as shown in figure. The smaller circle is tangent to the two bounding
radii and the arc of the sector. The radius of the smaller circle is
$\frac{r}{2}$
(b) $\frac{r}{3}$
(c) $\frac{2\sqrt{3}r}{5}$
(d) $\frac{r}{\sqrt{2}}$

Options

A. `r/2`
B. `r/3`
C. `(2sqrt3r)/5`
D. `r/sqrt2`

Answer

A

Explanation

Let the radius of smaller circle be x. Here,
`OP=xcosec30^@`
`andOQ=r=xcosec30^@`
`rArr =x=r/3`