From a point O inside a triangle ABC, perpendiculars OD, OE and OF are drawn to the sides BC, CA and AB, respectively. Prove that the perpendiculars from A, B and C to the sides EF, FD and DE are concurrentSolution in Tamil
Let the position vectors of points A,B,C,D,E and F be →a,→b,→c,→d,→eand→f w.r.t O. Let perpendiculars from A to EF and from B to DF meet each other at H. let position vectors of H be →r. We join CH. In order to prove the statement given in the question. it is sufficient it is sufficient to prove that CH is prependicular to DE.
Now asOD⊥BC⇒→d.(→b−→c)=0
⇒→d.→b=→d.→c
asOE⊥AC⇒→e.(→c−→a)=0⇒→e.→c=→e.→a
as OF⊥AB⇒→f.(→a−→b)=0⇒→f.→a=→f.→b
Also AH⊥EF⇒(→r.→a).(→e−→f)=0
⇒→r.→e−→r.→f−→a.→e+→a.→f=0
andBH⊥FD⇒(→r−→b).(→f−→d)=0
⇒→r.→f−→r.→d−→b.→f+→b.→d=0
Adding (iv) and (v) , we get
→r.→e−→a.→e+→a.→f−→r.→d−→b.→f+→b.→d=0
or→r.(→e.→d)−→e.→c+→d.→c=0 [ using (i), (ii) and (iii))]
or(→r−→c).(→e−→d)=0
⇒−−→CH.−−→ED=0⇒CH⊥ED
Topper's Solved these Questions
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGECHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Exercise 2.1
18 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGECHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Exercise 2.2
15 Videos
- CONIC SECTIONSBOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises
1255 Videos
- LIMITS AND DERIVATIVESBOOK - CENGAGECHAPTER - LIMITS AND DERIVATIVESEXERCISE - Solved Examples And Exercises
288 Videos
Similar Questions
Find |→a|and∣∣→b∣∣, if (→a+→b)⋅(→a−→b)=8and|→a|=8∣∣→b∣∣.
View SolutionIf →a=2ˆi+3ˆj−5ˆk,→b=mˆi+nˆj+12ˆkand→a×→b=→0 then find (m,n)
View SolutionLet A(0,1),B(1,1),C(1,−1),D(−1,0) be four points. If P is any other point, then PA+PB+PCPD≥d, when [d] is where [.] represents greatest integer.
View SolutionEvaluate the limit: (lim)x→0sinaxsinbx
View SolutionFrom a point O inside a triangle ABC, perpendiculars OD,OEandOf are drawn to rthe sides BC,CAandAB, respecrtively. Prove that the perpendiculars from A,B,andC to the sides EF,FDandDE are concurrent.
View SolutionFrom a point O inside a triangle ABC, perpendiculars OD, OE and OF are drawn to the sides BC, CA and AB, respectively. Prove that the perpendiculars from A, B and C to the sides EF, FD and DE are concurrent
View SolutionLet ABC and PQR be any two triangles in the same plane. Assume that the perpendiculars from the points A, B, C to the sides QR, RP, PQ respectively are concurrent. Using vector methods or otherwise,prove that the perpendiculars from P, Q, R to BC, CA, AB respectively are also concurrent.
View SolutionD,E,F are the foot of the perpendiculars from vertices A,B,C to sides BC,CA,AB respectively,and H is the or the centre of acute angled triangle ABC, where a,b,c are the sides of triangle ABC, then
View Solutionकिसी त्रिभुज ABC की भुजा BC,CA और AB के मध्यबिंदु क्रमशः D,E और F है। A से भुजा BC पर डाले गए लंब का चरण-बिंदु L है तो सिद्ध करें कि बिंदु D,E,F और L एकचक्रीय है।
View SolutionΔABC के अंदर बिंदु O से भुजाओ BC,CA और AB पर क्रमश: लंब OD,OE और OF डाले गए है। सिद्ध कीजिए कि
AF2+BD2+CE2=OA2+OB2+OC2−OD2−OE2−OF2.
View SolutionOn the outside of the equilateral triangle ABC and in the angular region ∠ABC, O is a point. OP, OQ and OR are the perpendiculars drawn from O to the sides. AB, BC and CA respectively. Prove that the height of the triangle = OP + OQ - OR.
View SolutionFrom a point O in the interior of a ΔABC perpendiculars OD, OE and OF are drawn to the sides BC, CA and AB respectively, then which one of the following is true ?
View SolutionFrom a point O inside a triangle ABC, perpendiculars OD,OEandOf are drawn to rthe sides BC,CAandAB, respecrtively. Prove that the perpendiculars from A,B,andC to the sides EF,FDandDE are concurrent.
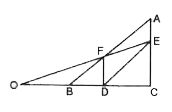
View Solutionयदि त्रिभुज ABC की भुजा BC पर कोई बिंदु D हैं। इस बिंदु से AC औरAB भुजाओं के समान्तर रेखाएं DF और DE खींची जाएं जो त्रिभुज की भुजा और AB को क्रमशः E तथा F पर काटती हैं। यदि EF और BC को आगे बढ़ाया जाए तो ये बिंदु O पर मिलती हैं। सिद्ध कीजिए कि OD2=OB.OC
View SolutionIf D, E and F are respectively the mid - points of sides BC, AC and AB of a ΔABC. If EF=3cm,FD=4cm and AB=10cm, then DE,BCandCA respectively will be equal to :
View Solution
