Let ABCD is a square with sides of unit length. Points E and F are taken om sides AB and AD respectively so that AE= AF. Let P be a point inside the square ABCD.The maximum possible area of quadrilateral CDFE is-Solution in Tamil
1/8
1/4
5/8
3/8
The correct Answer is:C
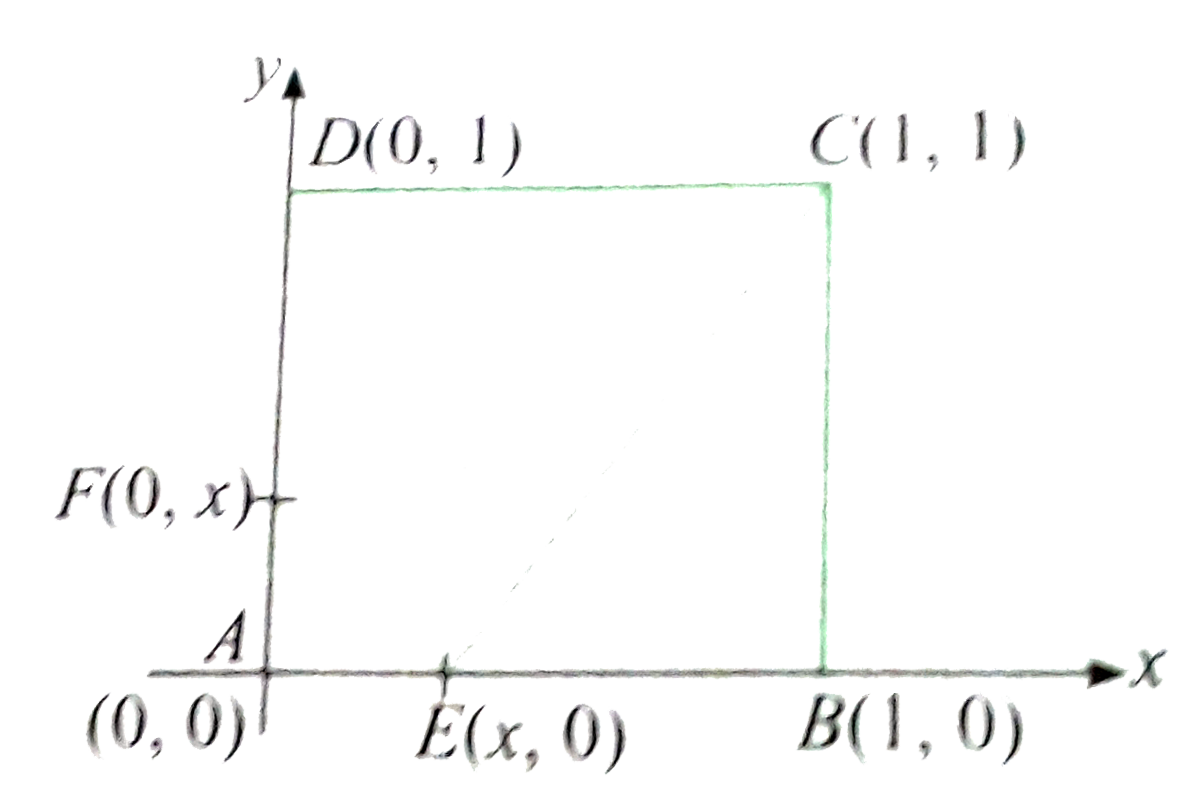
Area of CHEF
A=1−12x2−12(1−x)
=2−2x2−1+x2=1+x−x22=54−(x−12)22
Amax=58atx=12
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Matrix)
4 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Numerical)
12 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Multiple)
13 Videos
- COORDINATE SYSTEMBOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGECHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
Consider the triangle whose vertices are (-1,0),(5,-2) and (8,2). Find the centroid of the triangle.
View SolutionLine AB passes through point (2,3) and intersects the positive x and y-axes at A(a,0) and B(0,b) respectively. If the area of ΔAOB is 11. then the value of 4b2+9a2 is
View SolutionIf (−6,−4),(3,5),(−2,1) are the vertices of a parallelogram, then the remaining vertex can be (0,−1) (b) 7,9) (−1,0) (d) (−11,−8)
View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
View SolutionLet ABCD is a square with sides of unit length. Points E and F are taken om sides AB and AD respectively so that AE=AF .Let P be a point inside the square ABCD.The maximum possible area of quadrilateral CDFE is-
View SolutionLet ABCD be a square with sides of unit lenght. Points E and F are taken on sides AB and AD, respectively,so that AE=AF. Let P be a point inside the squre ABCD.
The value of (PA)2−(PB)2+(PC)2−(PD)2 is equal to
View SolutionLet ABCD be a square with sides of unit lenght. Points E and F are taken on sides AB and AD, respectively,so that AE=AF. Let P be a point inside the squre ABCD.
Let a line passing through point A divides the sqaure ABD into two parts so that the area of one portion is double the other. then the length of the protion of line inside the square is
View Solutionएक वर्ग ABCD की भुजा AB का मध्य बिंदु F है तथा बिंदु E भुजा BC पर इस प्रकार है की BE=13BC है|यदि ΔFBE का क्षेत्रफल 108 वर्ग सेमि. हो तो विकर्ण AC की लम्बाई ज्ञात करो |
View SolutionLet ABCD is a square with sides of unit lenghts . Points E and F are taken on sides AB and AD respectively so that AE =AF . Let P be a point inside the square ABCD.
The maximum area of quandrilateral CDFE will be -
View SolutionLet ABCD is a square with sides of unit lenghts . Points E and F are taken on sides AB and AD respectively so that AE =AF . Let P be a point inside the square ABCD.
The value of (PA)2−(PB)2+(PC)2−(PD)2 is equal to -
View SolutionLet ABCD is a square with sides of unit lenghts . Points E and F are taken on sides AB and AD respectively so that AE =AF . Let P be a point inside the square ABCD. Let a line passing throught point A divides the square ABCD into two parts so that area of one part is double to another , then lenght of the line segment inside the square is -
View SolutionLet ABCD be a quadrilateral with area 18, with side AB parallel to the side CD and AB = 2 CD. Let AD be perpendicular to AB and CD. If a circle is drawn inside the quadrilateral ABCD touching all the sides, then its radius is :
View SolutionABCD একটি 1 একক বাহুবিশিষ্ট বর্গক্ষেত্র। AB এবং AD- এর ওপর E এবং F বিন্দু দুটি এমনভাবে নেওয়া হল যেখানে AE=AF হয়। মনে করো ABCD বর্গক্ষেত্রের ভিতরে P একটি বিন্দু। CDFE- এর বৃহত্তম সম্ভাব্য ক্ষেত্রফল হবে-
View SolutionLet ABCD be a square with sides of unit lenght. Points E and F are taken on sides AB and AD, respectively,so that AE=AF. Let P be a point inside the squre ABCD.
The value of (PA)2−(PB)2+(PC)2−(PD)2 is equal to
View Solution
