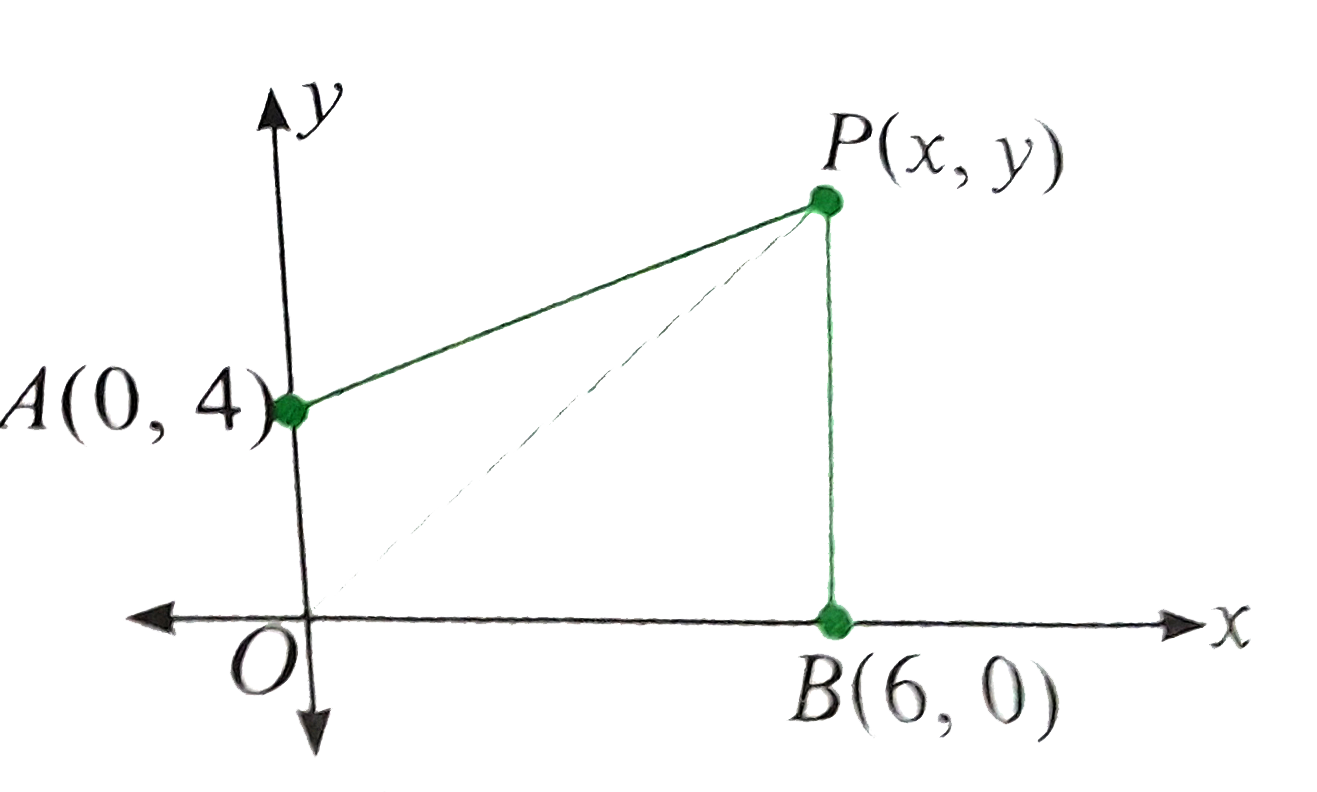
Let 0≡(0,0),A≡(0,4),B≡(6,0). Let P be a moving point such that the area of triangle POA is two times the area of triangle POB . The locus of P will be a straight line whose equation can be x+3y=0 (b) x+2y=0 2x−3y=0 (d) 3y−x=0Solution in Tamil
x+3y=0
x+2y=0
2x−3y=0
3y−x=0
The correct Answer is:A, D
Let point P be (x,y).
arΔPOA=12(OA)|x|=2|x|
arΔPOA=12(OB)|y|=3|y|
∴2|x|=6|y|
or |x|=3|y| or 3y−x=0or3y+x0
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Comprehension)
10 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Matrix)
4 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Single)
59 Videos
- COORDINATE SYSTEMBOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGECHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
Study the diagram. The line l is perpendicular to line m Does PE bisect CG?
View SolutionConsider the triangle whose vertices are (-1,0),(5,-2) and (8,2). Find the centroid of the triangle.
View SolutionABC is an isosceles triangle. If the coordinates of the base are B(1,3) and C(−2,7) , the coordinates of vertex A can be (a)(1,6) (b) (−12,5) (c)(56,6) (d) none of these
View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
View SolutionLet 0≡(0,0),A≡(0,4),B≡(6,0). Let P be a moving point such that the area of triangle POA is two times the area of triangle POB . The locus of P will be a straight line whose equation can be
View SolutionThe coordinates of three points O, A, B are (0, 0), (0,4) and (6, 0) respectively. A point P moves so that the area of ΔPOA is always twice the area of ΔPOB. Find the equation to both parts of the locus of P.
View SolutionGiven A(6,0) and B(0,4) and O is the origin.If the locus P such that area of ΔPOB=2 (area of ΔPOA ) is x2−ky2=0 ,then k is equal to
View SolutionThe sides of a triangle are 3x+2y−6=0,2x−3y+6=0,x+2y+2=0. P(0,b) is a point on y-axis. If P lies on the triangle or inside the triangle then the range of b is
View SolutionLet O be the origin and A, B be the two points having coordinates (0, 4) and (6, 0) respectively. If a point P moves in such a way that the area of the ΔOPA is always twice the area of ΔPOB, then P lies on
View SolutionLet O≡(0,0),A≡(0,4),B≡(6,0). Let P be a moving point such that the area of triangle POA is two times the area of triangle POB . The locus of P will be a straight line whose equation can be
View SolutionLet 0≡(0,0),A≡(0,4),B≡(6,0). Let P be a moving point such that the area of triangle POA is two times the area of triangle POB . The locus of P will be a straight line whose equation can be x+3y=0 (b) x+2y=0 2x−3y=0 (d) 3y−x=0
View SolutionLet P and Q be any two points on the lines represented by 2x−3y=0 and 2x+3y=0 respectively. If the area of triangle OPQ (where O is origin) is 5, then which of the following is not the possible equation of the locus of mid-point of PO?
View SolutionThe area of the triangle formed by the lines x + y - 3 = 0, x - 3y + 9 = 0 and 3x - 2y + 1 = 0 is -
View SolutionO(0,0),A(4,0),B(0,6) are the points. If P is a point such that the area of ΔPOB is twice the area of ΔPOA, then the locus of P is
View SolutionThe lines 2x + 3y-1 = 0, x + 2y-1 = 0 and ax + by -1 = 0 form a triangle whose perpendicular point is, then the value of (a, b) is
View Solution
