Let P and Q be any two points on the lines represented by 2x−3y=0 and 2x+3y=0 respectively. If the area of triangle OPQ (where O is origin) is 5, then which of the following is not the possible equation of the locus of mid-point of PO?
4x2−9y2+30=0
4x2−9y2−30=0
9x2−4y2−30=0
none of these
The correct Answer is:C
To solve the problem, we need to find the locus of the midpoint of the line segment OP, where P is a point on the line 2x−3y=0 and Q is a point on the line 2x+3y=0, given that the area of triangle OPQ is 5.
1. Identify Points P and Q:
- The line 2x−3y=0 can be rewritten as y=23x. Let P be a point on this line, represented as P(h,2h3).
- The line 2x+3y=0 can be rewritten as y=−23x. Let Q be a point on this line, represented as Q(k,−2k3).
2. Calculate the Area of Triangle OPQ:
- The area of triangle formed by points O(0,0), P(h,2h3), and Q(k,−2k3) can be calculated using the formula:
Area=12|x1(y2−y3)+x2(y3−y1)+x3(y1−y2)|
- Substituting the coordinates:
Area=12∣∣∣0(2h3+2k3)+h(−2k3−0)+k(0−2h3)∣∣∣
- This simplifies to:
Area=12∣∣∣−2hk3+2hk3∣∣∣=12∣∣∣−4hk3∣∣∣=2hk3
- Setting this equal to 5 (as given):
2hk3=5⟹hk=152
3. Find the Midpoint M of OP:
- The midpoint M of segment OP is given by:
M⎛⎝h2,2h32⎞⎠=(h2,h3)
4. Express h in terms of x and y:
- From the midpoint coordinates, we have:
x=h2⟹h=2x
y=h3⟹h=3y
- Equating the two expressions for h:
2x=3y⟹y=23x
5. Substituting h into the product hk:
- Since hk=152:
k=152h=152(2x)=154x
6. Finding the locus equation:
- Substitute h and k into the equation hk=152:
h⋅154x=152
- This leads to:
h=2x⟹2x⋅154x=152
- This gives:
15=15(which is always true)
7. Finding the locus of the midpoint:
- The locus of the midpoint can be derived from the equations obtained:
4x2−9y2−30=0
- This represents a hyperbola.
8. Identifying which equation is not possible:
- From the options given, we need to check which equation does not fit the derived locus equation.
Conclusion:
The locus of the midpoint of OP is represented by the equation 4x2−9y2−30=0. The options that do not match this form are the ones that are not possible equations of the locus.
- The line 2x−3y=0 can be rewritten as y=23x. Let P be a point on this line, represented as P(h,2h3).
- The line 2x+3y=0 can be rewritten as y=−23x. Let Q be a point on this line, represented as Q(k,−2k3).
- The area of triangle formed by points O(0,0), P(h,2h3), and Q(k,−2k3) can be calculated using the formula:
Area=12|x1(y2−y3)+x2(y3−y1)+x3(y1−y2)|
- Substituting the coordinates:
Area=12∣∣∣0(2h3+2k3)+h(−2k3−0)+k(0−2h3)∣∣∣
- This simplifies to:
Area=12∣∣∣−2hk3+2hk3∣∣∣=12∣∣∣−4hk3∣∣∣=2hk3
- Setting this equal to 5 (as given):
2hk3=5⟹hk=152
- The midpoint M of segment OP is given by:
M⎛⎝h2,2h32⎞⎠=(h2,h3)
- From the midpoint coordinates, we have:
x=h2⟹h=2x
y=h3⟹h=3y
- Equating the two expressions for h:
2x=3y⟹y=23x
- Since hk=152:
k=152h=152(2x)=154x
- Substitute h and k into the equation hk=152:
h⋅154x=152
- This leads to:
h=2x⟹2x⋅154x=152
- This gives:
15=15(which is always true)
- The locus of the midpoint can be derived from the equations obtained:
4x2−9y2−30=0
- This represents a hyperbola.
- From the options given, we need to check which equation does not fit the derived locus equation.
The locus of the midpoint of OP is represented by the equation 4x2−9y2−30=0. The options that do not match this form are the ones that are not possible equations of the locus.
Topper's Solved these Questions
- STRAIGHT LINEBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINEEXERCISE - Comprehension Type
3 Videos
- STRAIGHT LINEBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- STATISTICSBOOK - CENGAGE ENGLISHCHAPTER - STATISTICSEXERCISE - Archives
10 Videos
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE)
1 Videos
Similar Questions
A planet of mass m moves along an ellipse around the sun (mass M) so that its maxima and minimum distances from the sun are equal to r1 and r2 respectively. The angular momentum of this plane relative to the centre of the sun is m√PGMr1r28(r1+r2)
View SolutionTwo regression lines are represented by 2x+3y−10=0 and 4x+y−5=0
Find the line of regression of y on x.
View Solution
Knowledge Check
If P is the point (1,0) and Q is any point on the parabola y2=8x then the locus of mid - point of PQ is
AP1 lies on C2andQ1 lies on C1BPQ≥min{PP1,QQ1}Cpoint P0 on C1 such that P0Q0≤PQ for all pairs of points (P,Q) is (13,109)Dpoint Q0 on C2 such that P0Q0≤PQ for all pairs of points (P,Q) is (109,13)
If O is the origin and Q is a variable, point on x2=4y, find the locus of the mid-point of OQ.
View SolutionIf O is the origin and Q is a variable point on y2=x. Find the locus of the mid point of OQ.
View SolutionA and B are two points on the x-axis and y-axis respectively. P(2, -3) is the mid point of AB. Find the
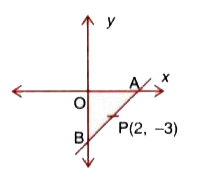
equation of line AB.
View SolutionA line is drawn through the point (1, 2) to meet the coordinate axes at P and Q such that it forms a triangle OPQ, where O is the origin. If the area of the triangle OPQ is least, then the slope of the line PQ is
View Solutionlet P be the point (1,0) and Q be a point on the locus y2=8x. The locus of the midpoint of PQ is
View SolutionThe tangent at any point P on y2=4x meets x-axis at Q, then locus of mid point of PQ will be
View SolutionLet the line y=mx intersects the curve y2=x at P and tangent to y2=x at P intersects x-axis at Q. If area (△OPQ) = 4, find m(m>0).
View Solution
