The vertices of a triangle are A(−1,−7),B(5,1)andC(1,4). If the internal angle bisector of ∠B meets the side AC in D, then find the length AD.Solution in Tamil
The angle bisector of ∠B meets the opposite side in D.
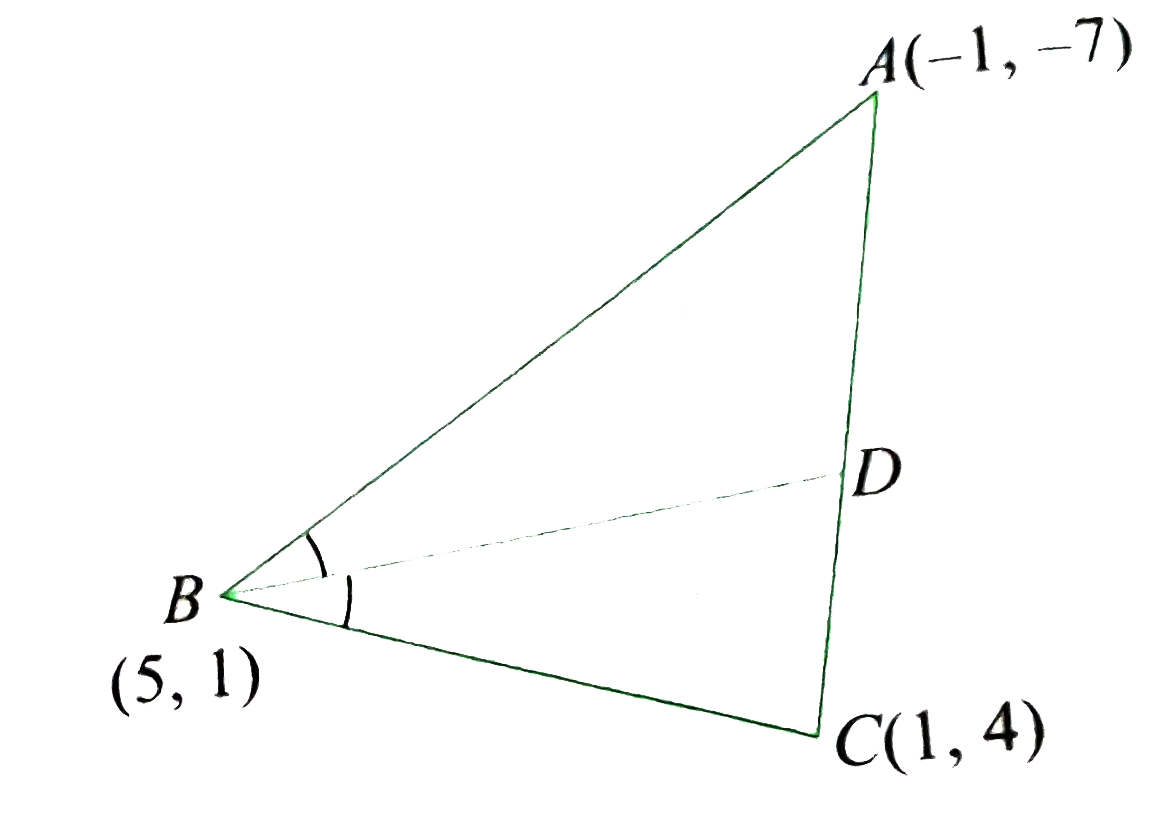
Using angle bisector theorem , we have
AD:DC=AB:BC
Now, AB=√(5+1)2+(1+7)2=10
and BC=√(5−1)2+(1−4)2=5
∴D=(2(1)+1(−1)2+1,2(4)+1(−7)2+1)=(13,13)
∴BD=√(5−13)2+(1−13)2=10√23
Topper's Solved these Questions
- COORDINATE SYSYEM Book:CENGAGEChapter:COORDINATE SYSYEM Exercise:Exercise 1.1
Explore 6 Videos
- COORDINATE SYSYEM Book:CENGAGEChapter:COORDINATE SYSYEM Exercise:Exercise 1.2
Explore 8 Videos
- COORDINATE SYSTEMBook:CENGAGEChapter:COORDINATE SYSTEMExercise:Multiple Correct Answers Type
Explore 2 Videos
- CROSS PRODUCTS Book:CENGAGEChapter:CROSS PRODUCTS Exercise:DPP 2.2
Explore 13 Videos
Similar Questions
What is the minimum area of a triangle with integral vertices ?
View SolutionThe distance between the points (acosα,asinα) and (acosβ,asinβ) is
View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
View SolutionThe vertices of a triangle are A(−1,−7),B(5,1)andC(1,4). If the internal angle bisector of ∠B meets the side AC in D, then find the length AD.
View SolutionThe vertices of a triangle are (A(−1,−7),B(5,1), and C(1,4). The equation of the bisector of ∠ABC is____
View SolutionThe vertices of a triangle are A(-1,-7),B(5,1) and C(1,4). The equation of the bisector of the angle ABC
View SolutionThe vertices f the triangle are A(5,4,6), B(1,−1,3)nad C(4,3,2). The internal bisector of angle A meets BC at D. Find the coordinates of D and the length AD.
View SolutionA(1,3,0),B(2,2,1) and C(5,−1,4) are the vertices of the triangle ABC, if the bisector of ∠BAC meets its side ¯¯¯¯¯¯BC at D, then find the coordinates of D.
View SolutionThe vertices of a triangle are A(−1,−7),B(5,1)andC(1,4). If the internal angle bisector of ∠B meets the side AC in D, then find the length AD.
View SolutionThe vertices of a triangle are A(−1,−7),B(5,1)andC(1,4). If the internal angle bisector of ∠B meets the side AC in D, then find the length AD.
View SolutionThe vertices of a triangle are (A(−1,−7),B(5,1), and C(1,4). The equation of the bisector of ∠ABC is____
View SolutionThe vertices of a triangle are A(−1,−7),B(5,1)andC(1,4). If the internal angle bisector of ∠B meets the side AC in D, then find the length AD.
View SolutionFind the equation of the bisector of angle A ofthe triangle whoe vertices are A(4,3),B(0,0)andC(2,3).
View SolutionABC is a triangle in which ∠A=720, the internal bisectors of angles B and C meet in O. Find the magnitude of ∠BOC
View SolutionIn a triangle ABC, the internal bisectors of ∠B and ∠C meet at P and the external bisectors of ∠B and ∠C meet at Q . Prove that ∠BPC+ ∠BQC=1800
View Solution
