The vertices of a triangle are A(−1,−7),B(5,1)andC(1,4). If the internal angle bisector of ∠B meets the side AC in D, then find the length AD.
The angle bisector of ∠B meets the opposite side in D.
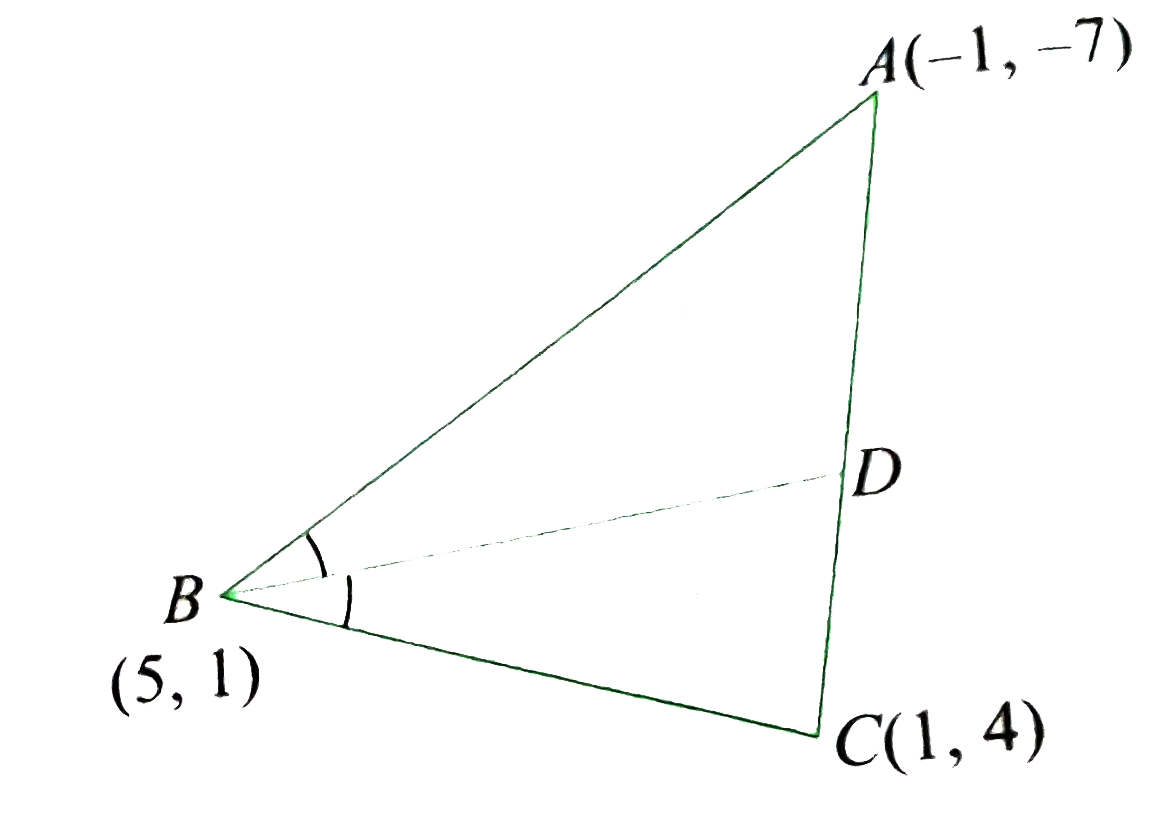
Using angle bisector theorem , we have
AD:DC=AB:BC
Now, AB=√(5+1)2+(1+7)2=10
and BC=√(5−1)2+(1−4)2=5
∴D=(2(1)+1(−1)2+1,2(4)+1(−7)2+1)=(13,13)
∴BD=√(5−13)2+(1−13)2=10√23
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.38
1 Video
- COORDINATE SYSYEM BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.39
1 Video
- COORDINATE SYSYEM BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.36
1 Video
- COORDINATE SYSTEMBOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGE ENGLISHCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
Knowledge Check
The vertices of a triangle are A(1, 3, 2), B(2, -1, 3) and C(-1, 4, 2). Find the angle A.
Acos−1(−√25)Bcos−1(−1√5)Csin−1(−√25)DNone of these
The vertices of a triangle are A(10,4),B(−4,0)andC(−2,8). Find the equation of its altitudes.
View SolutionThe vertices f the triangle are A(5,4,6), B(1,−1,3)nad C(4,3,2). The internal bisector of angle A meets BC at D. Find the coordinates of D and the length AD.
View SolutionThe vertices of a triangle are A(1,1,2), B (4,3,1) and C (2,3,5). The vector representing internal bisector of the angle A is
View SolutionTwo vertices of a triangle are (3,−5)and(−7,4). If its centroid is (2,−1), find the third vertiex.
View SolutionIn a triangle ABC, the internal angle bisector of ∠ABC meets AC at K. If BC=2,CK=1andBK=3√22, then find the length of side AB.
View SolutionABC is a triangle and the internal angle bisector of angle A cuts the side BC at D. If A=(3,-5), B(-3,3), C=(-1,-2) then find the length AD
View SolutionThe mid-points of the sides of a triangle are (1,5,−1),(0,4,−2)and(2,3,4). Find its vertices.
View Solution
