A line is drawn through the point (1, 2) to meet the coordinate axes at P and Q such that it forms a triangle OPQ, where O is the origin. If the area of the triangle OPQ is least, then the slope of the line PQ is Solution in Tamil
−14
-4
-2
−12
The correct Answer is:C
(y-2) = m(x-1)
∴OP=1−2m
OQ = 2-m
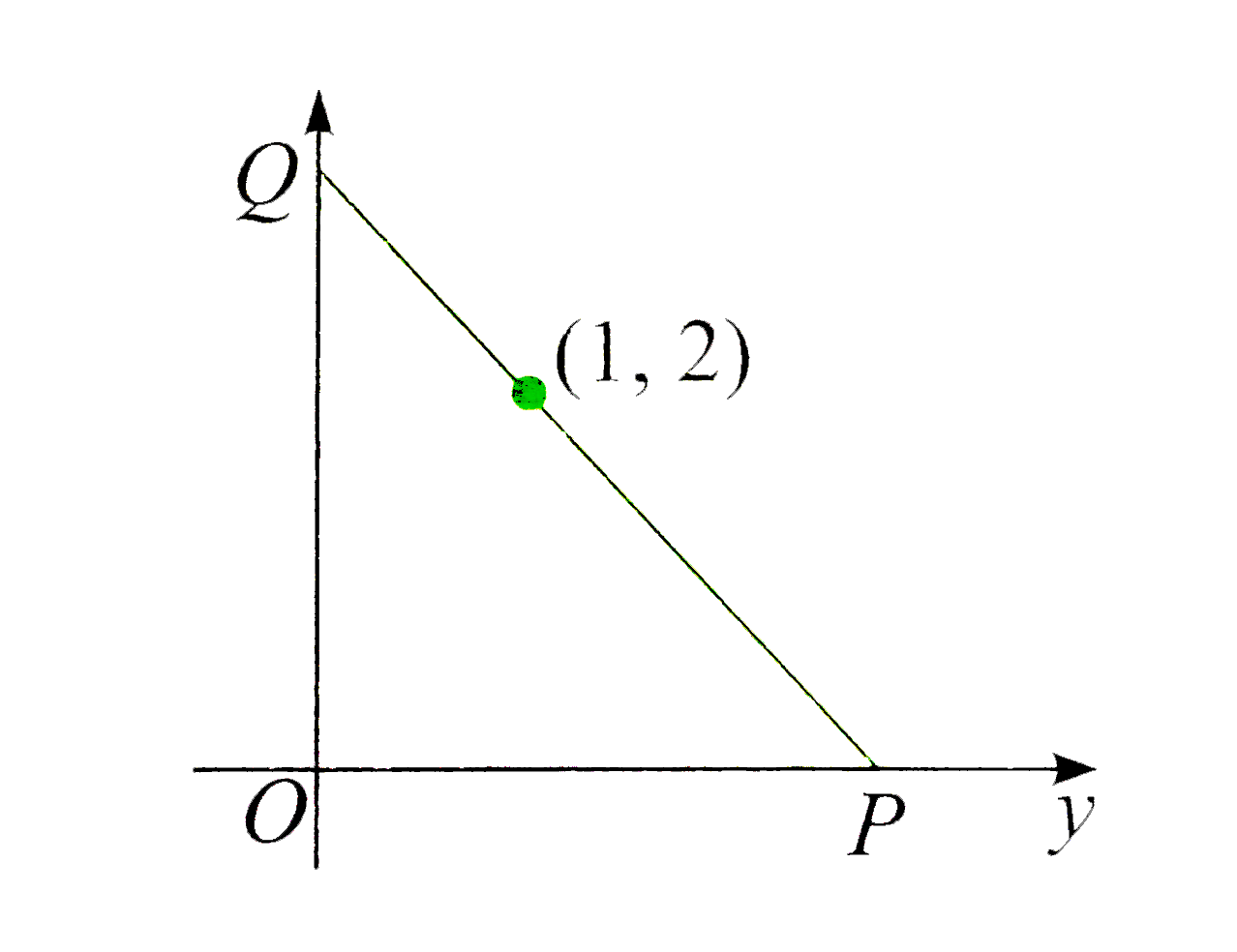
Area of ΔPOQ
=12(OP)(OQ)=12(1−2m)(2−m)
=12[2−m−4m+2]
=12[4−(m+4m)]
=12⎡⎣(√−m−2√−m)2+8⎤⎦ (∵m<0)
Which has least value when m =-2.
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - JEE Advanced Previous Year
4 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Numerical)
13 Videos
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year
9 Videos
Similar Questions
about to only mathematics
View Solutionstraight line L with negative slope passes through the point (9,4) cuts the positive coordinate axes at the point P and W As L. Varies, find the minimum value of |OP|+|OQ| , where O is origin .
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionQ. Let p and q real number such that p≠0,p2≠q and p2≠−q. if α and β are non-zero complex number satisfying α+β=−p and α3+β3=q, then a quadratic equation having αβ and βα as its roots is
View Solutionif P,Q are two points on the line 3x+4y+15=0 such that OP=OQ=9 then the area of triangle OPQ is
View SolutionA straight line intersect x and y axes at P and Q respectively. If (3, 5) is the middle point of PQ, then what is the area of the triangle OPQ ?
View SolutionLet O(0, 0), P(3, 4), Q(6, 0) be the vertices of the triangle OPQ. The point R inside the triangle OPQ is such that the triangles OPR, PQR are of equal area. The coordinates of R are
View Solutionबिंदु (1, 2) से खींची गई एक रेखा निर्देशांक अक्षों को P और Q पर मिलती है तथा अक्षों से त्रिभुज OPQ बनाती है, जहां O मूलबिंदु OPQ का क्षेत्रफल न्यूनतम हो, तो रेखा का ढाल है :
View SolutionIf the tangent at any point on the ellipse x2a2+y2b2=1 intersects the coordinate axes at P and Q , then the minimum value of the area (in square unit ) of the triangle OPQ is (O being the origin )-
View Solutionमाना (h,k) स्थिर बिंदु है जहां h>0,k>0, बिंदु (h,k) से जानेवाली सरल रेखा निर्देशांक अक्षों के बिंदु P तथा Q पर प्रतिच्छेद करती है। O मूलबिंदु हो तो ΔOPQ का निम्नतम क्षेत्रफल होगा
View Solution∆OPQ- এর শীর্ষবিন্দুগুলির স্থানাঙ্ক O (0,0), P (3,4), Q (6,0) ত্রিভুজটির ক্ষেত্রফল নির্ণয় কর।
View SolutionA line is drawn through the point (1,2) to meet the coordinate axes at P and Q such that it forms a triangle OPQ ,where 0 is the origin.If the area of the triangle OPQ is least,the slope of the line PQ is k ,then |k|=
View SolutionA straight line passing through the point (87, 33) cuts the positive direction of the coordinate axes at the point P and Q. If Q is the origin then the minimum area of the triangle OPQ is.
View Solutionमाना त्रिभुज OPQ के शीर्ष O(0,0), P(3,4),Q(6,0) है। बिन्दु R, त्रिभुज OPQ के अन्दर इस प्रकार हैं कि त्रिभुज OPR, PQR, OQR बराबर क्षेत्रफल के हैं। तब R के निर्देशांक है
View Solutionif P,Q are two points on the line 3x+4y+15=0 such that OP=OQ=9 then the area of triangle OPQ is
View SolutionA line is drawn through the point (1,2) to meet the co-ordinate axes at P and Q such that it forms a Δ1e OPQ, where O is the origin. If the area of the Δ OPQ, is least, then the slope of the line PQ is
View Solution
