The line L1:y−x=0 and L2:2x+y=0 intersect the line L3:y+2=0 at P and Q respectively. The bisector of the acute angle between L1 and L2 intersects L3 at R. Statement-1 : The ratio PR:RQ equals 2√2:√5 Statement-2 : In any triangle, bisector of an angle divides the triangle into two similar triangles. Statement-1 is true, Statement-2 is true ; Statement-2 is correct explanation for Statement-1 Statement-1 is true, Statement-2 is true ; Statement-2 is not a correct explanation for Statement-1 Statement-1 is true, Statement-2 is false Statement-1 is false, Statement-2 is trueSolution in Tamil
Statement 1 is true, statement 2 is false.
Statement 1 is true, statement 2 is true, statement 2 is the correct explanation of statement1.
Statement 1 is true, statement 2 is true, statement 2 is not the correct explanation of statement 1.
Statement 1 is false, statement 2 is true.
The correct Answer is:A
Draw lines on coordinate axes as shown here.
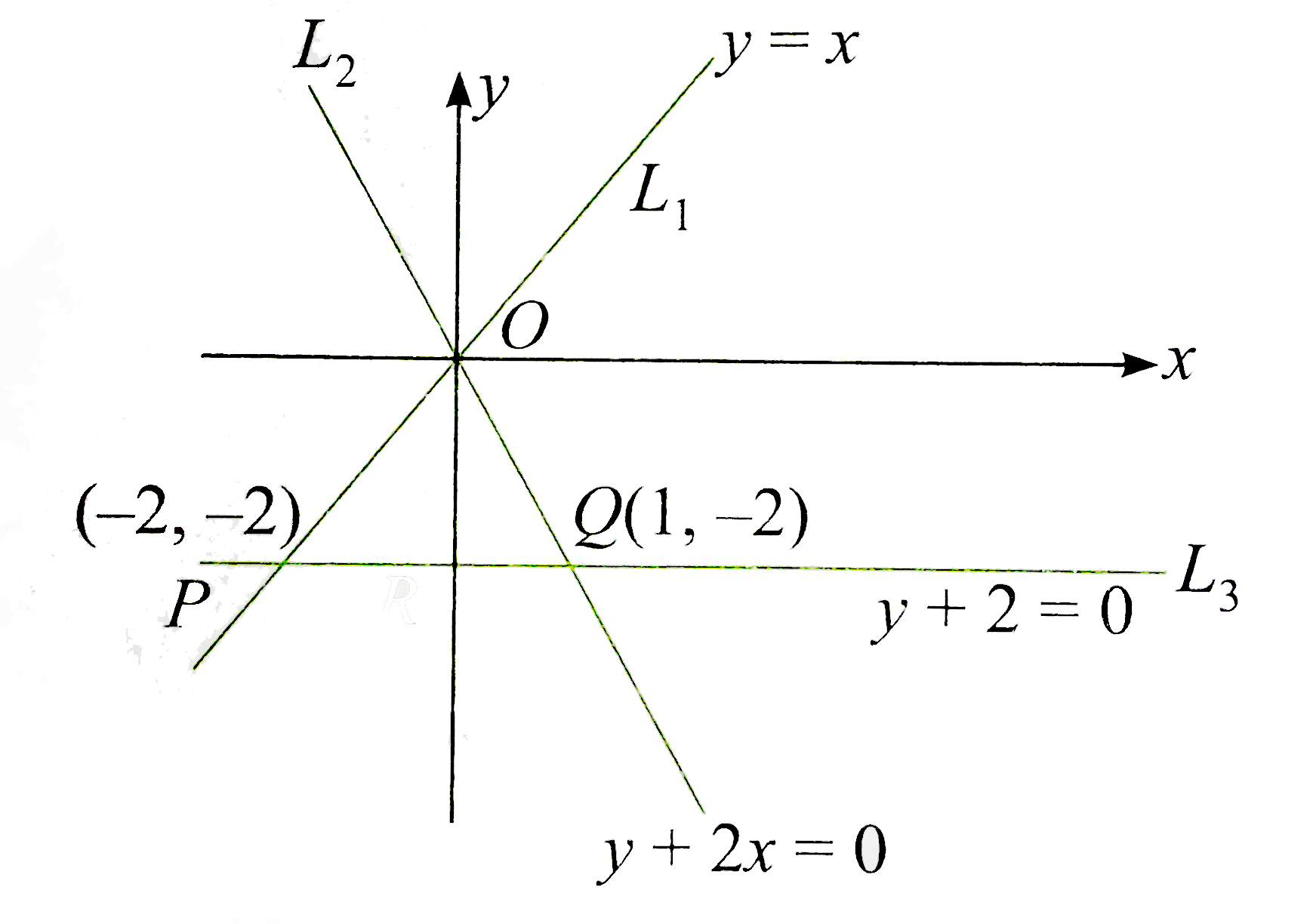
From the geometry of angle bisector,
PRRQ=OPOQ=2√2√5
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - JEE Advanced Previous Year
4 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Numerical)
13 Videos
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year
9 Videos
Similar Questions
about to only mathematics
View Solutionstraight line L with negative slope passes through the point (9,4) cuts the positive coordinate axes at the point P and W As L. Varies, find the minimum value of |OP|+|OQ| , where O is origin .
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionQ. Let p and q real number such that p≠0,p2≠q and p2≠−q. if α and β are non-zero complex number satisfying α+β=−p and α3+β3=q, then a quadratic equation having αβ and βα as its roots is
View SolutionConsider: L1:2x+3y+p−3=0 L2:2x+3y+p+3=0 where p is a real number and C:x2+y2+6x−10y+30=0 Statement 1 : If line L1 is a chord of circle C, then line L2 is not always a diameter of circle C. Statement 2 : If line L1 is a a diameter of circle C, then line L2 is not a chord of circle C. (A) Both the statement are True and Statement 2 is the correct explanation of Statement 1. (B) Both the statement are True but Statement 2 is not the correct explanation of Statement 1. (C) Statement 1 is True and Statement 2 is False. (D) Statement 1 is False and Statement 2 is True.
View SolutionSTATEMENT-1 : The graph of y=[√1−cos2x) consists of only two line segments. where [.] represent greatest integer function. AND STATEMENT-2: The graph of √y=1−cos2x is STATEMENT-1 is true, STATEMENT-2 is true and STATEMENT-2 is correct explanation for STATEMENT-1 STATEMENT-1 is true, STATEMENT-2 is true and STATEMENT-2 is not correct explanation for STATEMENT-1 STATEMENT-1 is true, STATEMENT-2 is false STATEMENT-1 is false, STATEMENT-2 is true Both STATEMENTS are false
View SolutionThe lines L_(1): y-x=0 " and " L_(2): 2x+y=0 intersect the line L_(3):y+2=0 at P and Q, respectively. The bisector of the acute angle between L_(1) " and " L_(2) " intersects " L_(3) at R. Statement 1 : The ratio PR : RQ equals 2sqrt(2) : sqrt(5). Statement 2: In any triangle, bisector of an angle divides the triangle into two similar triangles.1
View SolutionLines L_(1) : y-c=0 and L_(2) : 2x+y=0 intersect the line L_(3) : y+2=0 at P and Q respectively. The bisector of the acute angle between L_(1) and L_(2) intersects L_(3) at R . Statement I The ratio PR : RQ equals 2sqrt(2) : sqrt(5) . Because Statement II In any triangle, bisector of an angle divides the triangle into two similar triangles.
View SolutionThe lines L_(1) : y - x = 0 and L_(2) : 2x + y = 0 intersect the line L_(3) : y + 2 = 0 at P and Q respectively . The bisectors of the acute angle between L_(1) and L_(2) intersect L_(3) at R . Statement 1 : The ratio PR : RQ equals 2sqrt2 : sqrt5 Statement - 2 : In any triangle , bisector of an angle divides the triangle into two similar triangles .
View SolutionThe line L1:y−x=0 and L2:2x+y=0 intersect the line L3:y+2=0 at P and Q respectively. The bisector of the acute angle between L1 and L2 intersects L3 at R. Statement-1 : The ratio PR:RQ equals 2√2:√5 Statement-2 : In any triangle, bisector of an angle divides the triangle into two similar triangles. Statement-1 is true, Statement-2 is true ; Statement-2 is correct explanation for Statement-1 Statement-1 is true, Statement-2 is true ; Statement-2 is not a correct explanation for Statement-1 Statement-1 is true, Statement-2 is false Statement-1 is false, Statement-2 is true
View SolutionConsider: L1:2x+3y+p−3=0 L2:2x+3y+p+3=0 where p is a real number and C:x2+y2+6x−10y+30=0 Statement 1 : If line L1 is a chord of circle C, then line L2 is not always a diameter of circle C. Statement 2 : If line L1 is a a diameter of circle C, then line L2 is not a chord of circle C. (A) Both the statement are True and Statement 2 is the correct explanation of Statement 1. (B) Both the statement are True but Statement 2 is not the correct explanation of Statement 1. (C) Statement 1 is True and Statement 2 is False. (D) Statement 1 is False and Statement 2 is True.
View SolutionThe lines L_(1) : y - x = 0 and L_(2) : 2x + y = 0 intersect the line L_(3) : y + 2 = 0 at P and Q respectively . The bisectors of the acute angle between L_(1) and L_(2) intersect L_(3) at R . Statement 1 : The ratio PR : RQ equals 2sqrt2 : sqrt5 Statement - 2 : In any triangle , bisector of an angle divides the triangle into two similar triangles .
View SolutionLines L_(1):y-x=0 and L_(2):2x+y=0 intersect the line L_(3) : y+2=0 at P and Q respectively. The bisector of the acute angle between L_(1) and L_(2) intersects L_(3) at R. Statement-I: The ratio PR: RQ equals 2sqrt(2):sqrt(5) because. Statement II: In any triangle bisector of an angle divides the triangle into two similar triangles.
View SolutionThe lines L_1 :y-x =0 and L_2 : 2x+y =0 intersect the line L_3 : y+2 =0 at P and Q respectively. The bisector of the acute angle between L_1 and L_2 intersects L_3 at R Statement - 1 : The ratio PR : PQ equals 2sqrt2 : sqrt5 Statement - 2 : In any triangle , bisector of an angle divides the triangle into two similar triangle
View SolutionStatement-1 :Perpendicular from origin O to the line joining the points A(osα,csinα) and B(osβ,csinβ) divides it in the ratio 1:1 Statement-2 Perpendicular from opposite vertex to the base of an isosceles triangle bisects it Statement-1 is True, Statement-2 is True; Statement-2 is a correct explanation for Statement-1 Statement-1 is True, Statement-2 is True; Statement-2 is not a correct explanation for Statement-1 Statement-1 is True, Statement-2 is False Statement-1 is False, Statement-2 is True
View SolutionStatement 1. In any triangle ABC,ifa:b:c=4:5:6,thenR:r=16:7, Statement 2. In any triangle Rr=abc4s (A) Both Statement 1 and Statement 2 are true and Statement 2 is the correct explanation of Statement 1 (B) Both Statement 1 and Statement 2 are true and Statement 2 is not the correct explanatioin of Statement 1 (C) Statement 1 is true but Statement 2 is false. (D) Statement 1 is false but Stastement 2 is true
View Solution
