Consider point A(6, 30), point B(24, 6) and line AB: 4x+3y = 114.
Point P(0,λ) is a point on y-axis such that 0<λ<38 and point Q(0,λ) is a point on y-axis such that λ>38.
For all positions of pont Q, and AQB is maximum when point Q isSolution in Tamil
(0, 54)
(0, 58)
(0, 60)
(0, 1)
The correct Answer is:B
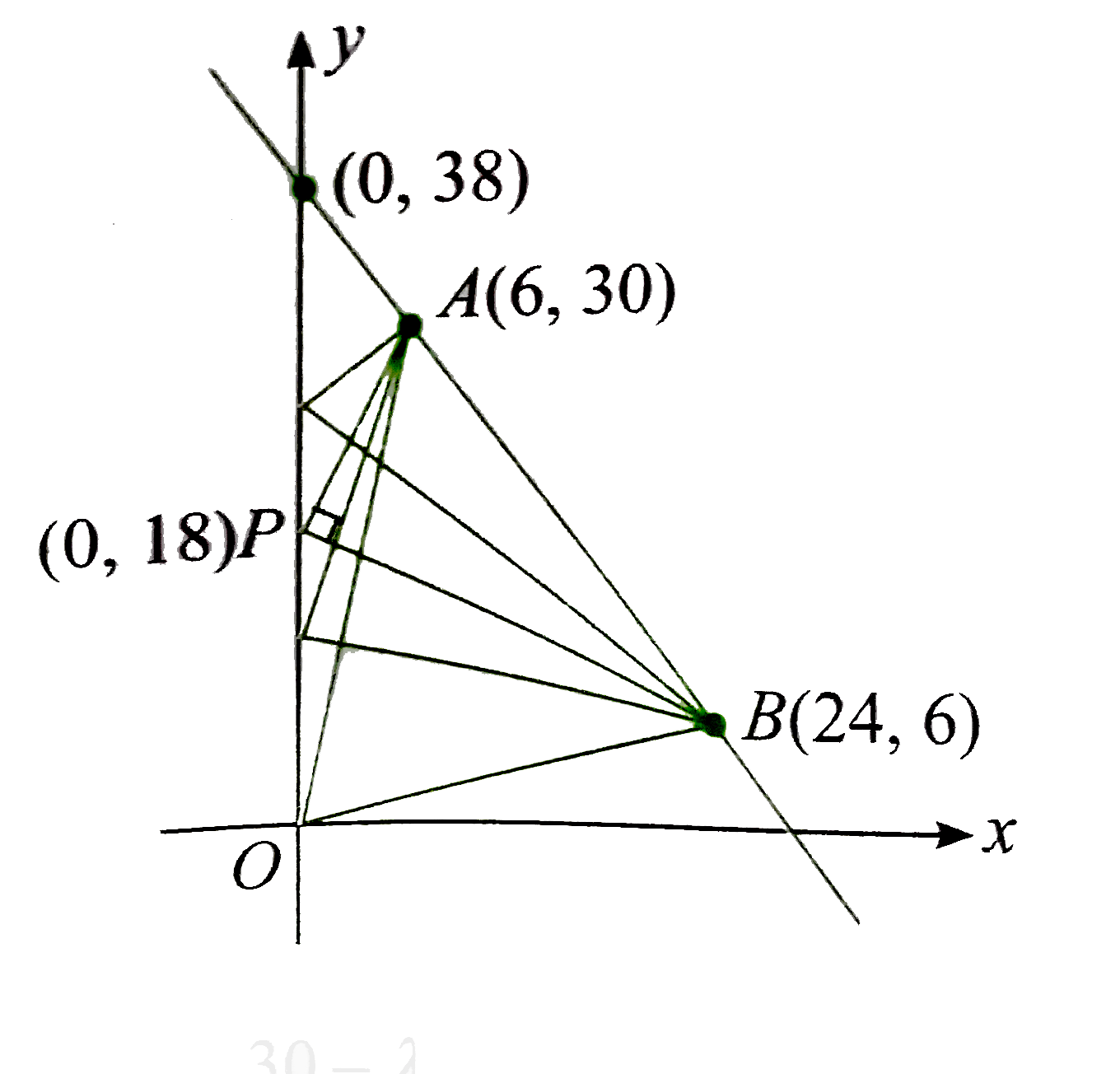
Slope of AP is m1=30−λ6
Slope of BP is m2=6−λ24
tanθ=30−λ6−6−λ241+(30−λ6)(6−λ24)
=720−24λ−36+6λ144+180−36λ+λ2
=18(38−λ)324−36λ+λ2=(38−λ)18(λ−18)2
Clearly, for 0<λ<38.
Maximum value of tanθ→∞ for which θ=π2,
Now, ddλ(tanθ)=18(18−λ)(λ−58)(λ−18)4
Clearly, λ=58 is point of maximum as derivative changes sign from '+' to '−'.
So, point Q≡(0,58) when ∠AQB is maximum.
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Matrix)
8 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Numerical)
13 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Multiple)
30 Videos
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year
9 Videos
Similar Questions
Consider the lines represented by equation (x2+xy−x)×(x−y)=0 forming a triangle. Then match the following lists:

View Solutionstraight line L with negative slope passes through the point (9,4) cuts the positive coordinate axes at the point P and W As L. Varies, find the minimum value of |OP|+|OQ| , where O is origin .
View SolutionIf P is a point (x,y) on the line y=−3x such that P and the point (3, 4) are on the opposite sides of the line 3x−4y=8, then x>815 (b) x>85 y<−85 (d) y<−815
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionQ. Let p and q real number such that p≠0,p2≠q and p2≠−q. if α and β are non-zero complex number satisfying α+β=−p and α3+β3=q, then a quadratic equation having αβ and βα as its roots is
View SolutionIf a circle passes through the point of intersection of the lines x+y+1=0 and x+lambda y-3=0 with the coordinate axis,then value of lambda is
View SolutionA light beam emanating from the point A(3,10) reflects from the straight line 2x+y-6=0 and then passes through the point B(4,3) .The equation of the reflected beam is x+3y-lambda=0, then the valueof lambda is
View SolutionIf the family of lines lambda x+3y-6=0(lambda is variable) intersect the lines x-2y+3=0 and x-y+1=0 in P and Q,then locus of the middle point of PQ is
View SolutionLocus of the image of the point (1,1) in the line (5x-2y-7)+lambda(2x-3y+6)=0 (lambda in R'), is
View SolutionConsider point A(6, 30), point B(24, 6) and line AB: 4x+3y = 114.
Point P(0,λ) is a point on y-axis such that 0<λ<38 and point Q(0,λ) is a point on y-axis such that λ>38.
For all positions of pont P, angle APB is maximum when point P is
View SolutionConsider point A(6, 30), point B(24, 6) and line AB: 4x+3y = 114.
Point P(0,λ) is a point on y-axis such that 0<λ<38 and point Q(0,λ) is a point on y-axis such that λ>38.
The maximum value of angle APB is
View SolutionConsider point A(6, 30), point B(24, 6) and line AB: 4x+3y = 114.
Point P(0,λ) is a point on y-axis such that 0<λ<38 and point Q(0,λ) is a point on y-axis such that λ>38.
For all positions of pont Q, and AQB is maximum when point Q is
View SolutionIf a circle passes through the point of intersection of the lines x+y+1=0 and x+λy−3=0 with the coordinate axis, then find the value of λ .
View SolutionConsider point A(6, 30), point B(24, 6) and line AB: 4x+3y = 114.
Point P(0,λ) is a point on y-axis such that 0<λ<38 and point Q(0,λ) is a point on y-axis such that λ>38.
For all positions of pont P, angle APB is maximum when point P is
View SolutionConsider point A(6, 30), point B(24, 6) and line AB: 4x+3y = 114.
Point P(0,λ) is a point on y-axis such that 0<λ<38 and point Q(0,λ) is a point on y-axis such that λ>38.
The maximum value of angle APB is
View SolutionConsider point A(6, 30), point B(24, 6) and line AB: 4x+3y = 114.
Point P(0,λ) is a point on y-axis such that 0<λ<38 and point Q(0,λ) is a point on y-axis such that λ>38.
For all positions of pont Q, and AQB is maximum when point Q is
View Solution
