The base of an isosceles triangle measures 4 units base angle is equal to $45^{\circ}$ . A straight line cuts the extension of the base at a point M at the angle $θ$ and bisects the lateral side of the triangle which is nearest to M.
The area of quadrilateral which the straight line cuts off from the given triangle is Solution in Tamil

A

$\frac{3 + tan θ}{1 + tan θ}$

B

$\frac{3 + 5 tan θ}{1 + tan θ}$

C

$\frac{3 + tan θ}{1 - tan θ}$

D

$\frac{3 + 2 tan θ}{1 + tan θ}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

For the given specification of the triangle, consider triangle ABC as shown in the figure.

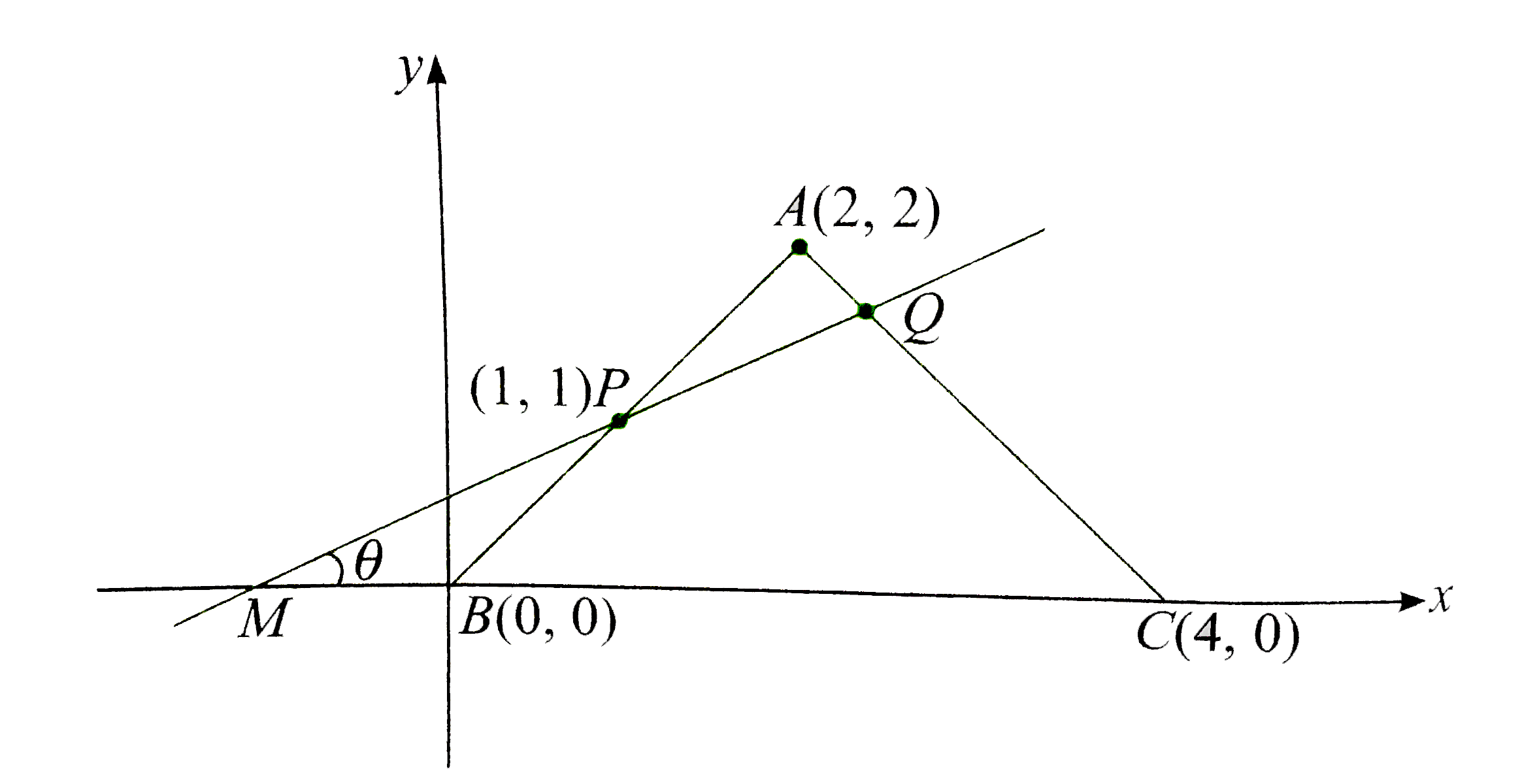
Equation of line PM is
$y - 1 = tan θ (x - 1)$
For point Q, solving MP and AC,
$4 - x - 1 = tan θ (x - 1)$
$\Rightarrow Q \equiv (\frac{3 + tan θ}{1 + tan θ}, \frac{1 + 3 tan θ}{1 + tan θ})$
$Area of Δ A P Q = \frac{1}{2} ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ \begin{matrix} 1 & 1 & 1 2 & 2 & 1 \frac{3 + tan θ}{1 + tan θ} & \frac{1 + 3 tan θ}{1 + tan θ} & 1 \end{matrix} ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ = \frac{1 - tan θ}{1 + tan θ} (As θ < π / 4)$
Area of quadilateral BPQC,
$Δ = \frac{1}{2} \times 4 \times 2 - (\frac{1 - tan θ}{1 + tan θ})$
$or Δ = (\frac{3 + 5 tan θ}{1 + tan θ})$
$or Δ = 5 - \frac{2}{1 + tan θ} where θ \in (0, \frac{π}{4})$
$∴ Δ \in (3, 4)$
${(P Q)}^{2} = {(\frac{3 + tan θ}{1 + tan θ} - 1)}^{2} + {(\frac{1 + 3 tan θ}{1 + tan θ} - 1)}^{2}$
$= \frac{4 (1 + {tan}^{2} θ)}{1 + {tan}^{2} θ + 2 tan θ}$
$= \frac{4}{1 + \frac{2 tan θ}{1 + {tan}^{2} θ}}$
$= \frac{4}{1 + sin 2 θ}$
$S o, {(P Q)}^{2} \in (2, 4)$
$∴ P Q \in (\sqrt{2}, 2)$

Updated on:21/07/2023

|

Class 12 MATHS STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

CENGAGE-STRAIGHT LINES-Exercise (Comprehension)

Home
Ask Doubt
Profile