The condition on a and b , such that the portion of the line ax+by−1=0 intercepted between the lines ax+y=0 and x+by=0 subtends a right angle at the origin, is (a)a=b (b) a+b=0 (c)a=2b (d) 2a=bSolution in Tamil
a =b
a+b=0
a=2b
2a=b
The correct Answer is:B
Lines ax+y=0 and x+by=0 intersect at O(0,0).
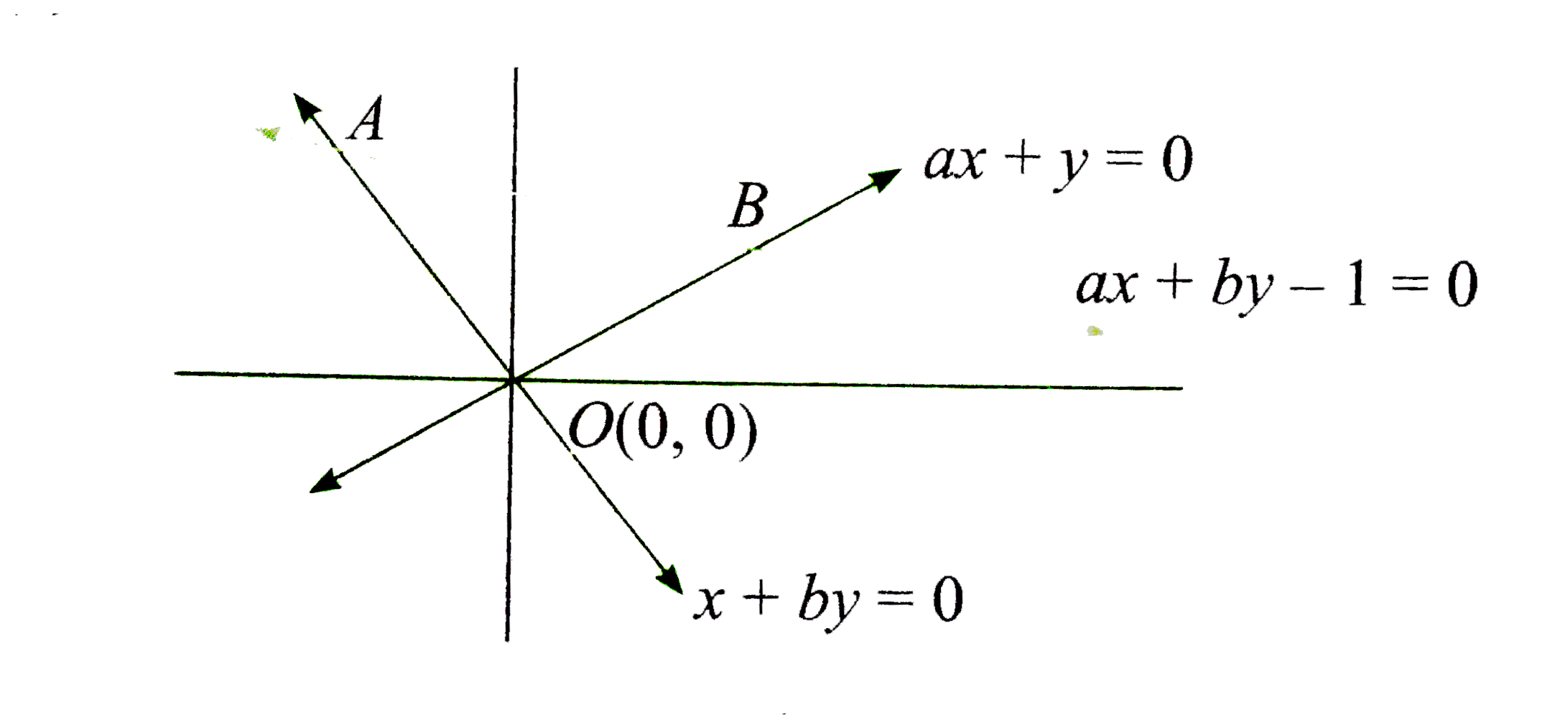
Hence, if AB subtends right angle at O(0,0), then ax+y=0 and x+by=0 are perpendicular to each other. So,
(−a)(−1b)=−1
or a+b=0
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Multiple)
30 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Comprehension)
27 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.6
5 Videos
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year
9 Videos
Similar Questions
If P is a point (x,y) on the line y=−3x such that P and the point (3, 4) are on the opposite sides of the line 3x−4y=8, then x>815 (b) x>85 y<−85 (d) y<−815
View SolutionLet L be the line belonging to the family of straight lines (a+2b) x+(a-3b)y+a-8b =0, a, b ∈R, which is the farthest from the point (2, 2).
Area enclosed by the line L and the coordinate axes is
View SolutionIf aandb are two arbitrary constants, then prove that the straight line (a−2b)x+(a+3b)y+3a+4b=0 will pass through a fixed point. Find that point.
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionQ. Let p and q real number such that p≠0,p2≠q and p2≠−q. if α and β are non-zero complex number satisfying α+β=−p and α3+β3=q, then a quadratic equation having αβ and βα as its roots is
View SolutionThe condition on a and b , such that the portion of the line ax+by−1=0 intercepted between the lines ax+y=0 and x+by=0 subtends a right angle at the origin, is a=b (b) a+b=0 a=2b (d) 2a=b
View SolutionThe portion of the line ax+by-1=0 intercepted between the lines ax+y+1=0 and x+by=0 subtends a right angle at the origin and the condition in a and b is lambda a+b+b^(2)=0, then find value of lambda
View SolutionIf the lines x+ay+a=0, bx+y+b=0 and cx+cy+1=0 are concurrent, then write the value of 2abc−ab−bc−ca.
View SolutionIf the portion of the line ax - by - 1 = 0 , intercepted between the lines ax + y + 1 = 0 and x + by = 0 subtends a right angle at the origin , then find value of 4a+b2+(b+1)2.
View SolutionShow that the straight lines (a−b)x+(b−c)y=c−a,(b−c)x+(c−a)y=a−b and (c−a)x+(a−b)y=b−c are concurrent.
View SolutionIf the line ax+by+c=0 is a normal to the curve xy=1, then a>0,b>0 a>0,b<0 a⟨0,b⟩0 (d) a<0,b<0 none of these
View SolutionThe condition on a and b , such that the portion of the line ax+by−1=0 intercepted between the lines ax+y=0 and x+by=0 subtends a right angle at the origin, is a=b (b) a+b=0 a=2b (d) 2a=b
View SolutionA circle with center (a,b) passes through the origin. The equation of the tangent to the circle at the origin is (a)ax−by=0 (b) ax+by=0 bx−ay=0 (d) bx+ay=0
View SolutionShow that the following lines are concurrent: L1=(a−b)x+(b−c)y+(c−a)=0 L2=(b−c)x+(c−a)y+(a−b)=0 L3=(c−a)x+(a−b)y+(b−c)=0
View SolutionIf the lines x+ay+a=0, bx+y+b=0 and cx+cy+1=0 are concurrent, then write the value of 2abc−ab−bc−ca.
View SolutionIf the line ax+by+c=0 is a normal to the curve xy=1, then a>0,b>0 a>0,b<0 a⟨0,b⟩0 (d) a<0,b<0 none of these
View Solution
