The lien x3+y4=1 meets the y− and x−axys at AandB , respectively. A square ABCD is constructed on the line segment AB away from the origin. The coordinates of the vertex of the square farthest from the origin are (7, 3) (b) (4, 7) (c) (6, 4) (d) (3, 8)Solution in Tamil
7,3
4,7
6,4
3,8
The correct Answer is:B
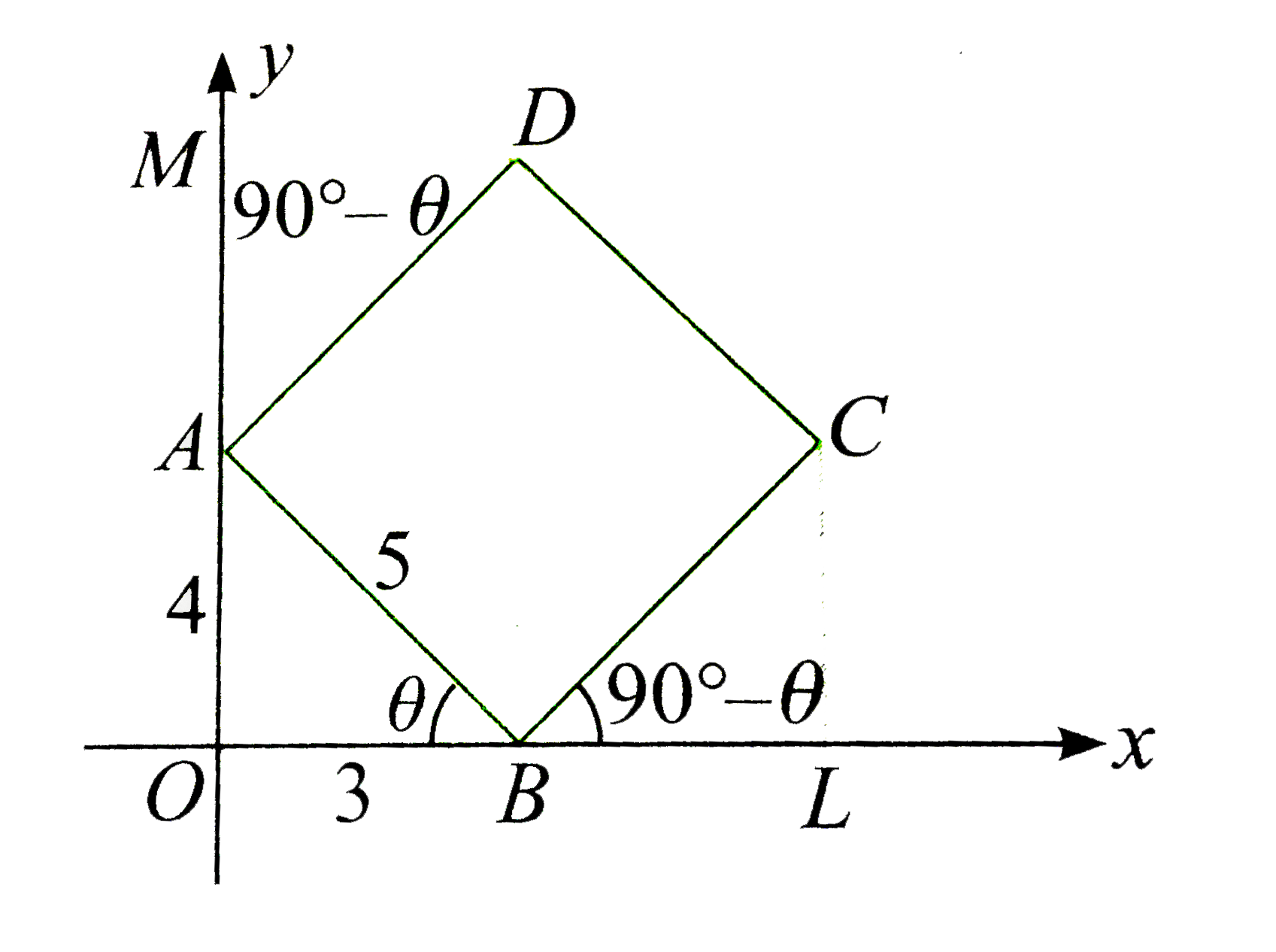
The coordinates of A are (0,4) and those of B are (3,0).
BC=AB=√32+42=5
or BL=BCsinθand CL=BCcosθ
or BL=5×45=4and
CL=5×35=3
Similarly, MD =4 and AM=3.
So, the coordinates of C are (OB+BL,CL) ≡(7,3) and those of D are (MD, OA+AM) ≡(4,7).
The coordinates of the vertex farthest from the origin are (4,7).
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Multiple)
30 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Comprehension)
27 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.6
5 Videos
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year
9 Videos
Similar Questions
If P is a point (x,y) on the line y=−3x such that P and the point (3, 4) are on the opposite sides of the line 3x−4y=8, then x>815 (b) x>85 y<−85 (d) y<−815
View SolutionLet L be the line belonging to the family of straight lines (a+2b) x+(a-3b)y+a-8b =0, a, b ∈R, which is the farthest from the point (2, 2).
Area enclosed by the line L and the coordinate axes is
View SolutionIf aandb are two arbitrary constants, then prove that the straight line (a−2b)x+(a+3b)y+3a+4b=0 will pass through a fixed point. Find that point.
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionQ. Let p and q real number such that p≠0,p2≠q and p2≠−q. if α and β are non-zero complex number satisfying α+β=−p and α3+β3=q, then a quadratic equation having αβ and βα as its roots is
View SolutionThe lien x3+y4=1 meets the y- and x-axis at A and B , respectively. A square ABCD is constructed on the line segment AB away from the origin. The coordinates of the vertex of the square farthest from the origin are (7, 3) (b) (4, 7) (c) (6, 4) (d) (3, 8)
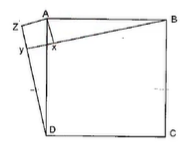
View SolutionIn Figure, X is a point in the interior of square ABCD. AXYZ is also a square. If DY=3 cm and AZ=2 cm, then BY=
(a) 5cm
(b) 6cm
(c) 7cm
(d) 8cm
View SolutionIf A={2, 3, 4} , B={1, 3, 7} and R={(x, y):x∈A, y∈B and x<y} is a relation from A to B , then write R−1 .
View SolutionThe perpendicular distance from the origin to the plane containing the two lines, x+23=y−25=z+57 and x−11=y−44=z+47 is: (a) 11√6 (b)11√6 (c) 11 (d) 6√11
View Solutionबिंदुओं A,B,C तथा D के निर्देशांक क्रमशः (6,3),(−3,5),(4,−2) तथा (x,y) है तो सिद्ध कीजिए कि △DBC△ABC=|x+y−2|7
View SolutionThe line x3+y4=1 meets the y-axis and x-axis at A and B respectively. A square ABCD is constructed on the line segment AB away from the origin. The coordinates of the vertex of the square farthest from the origin are
View SolutionThe foot of the perpendicular on the line 3x+y=λ drawn from the origin is C. If the line cuts the x and the y-axis at AandB , respectively, then BC:CA is 1:3 (b) 3:1 (c) 1:9 (d) 9:1
View SolutionIn ABC , the coordinates of the vertex A are (4,−1) , and lines x−y−1=0 and 2x−y=3 are the internal bisectors of angles BandC . Then, the radius of the encircle of triangle ABC is (a) 4√5 (b) 3√5 (c) 6√5 (d) 7√5
View SolutionIn Figure, X is a point in the interior of square ABCD. AXYZ is also a square. If DY=3 cm and AZ=2 cm, then BY=
(a) 5cm
(b) 6 cm
(c) 7 cm
(d) 8 cm
View SolutionThe line x3+y4=1 meets the axis of y and axis of x at A and B respectively A square ABCD is coonstructed on the line segment AB away from the origin, the coordinates of the vertex of the square farthest from the origin are
View Solution
