x−y≤2Solution in Tamil
The correct Answer is:3 sq. units
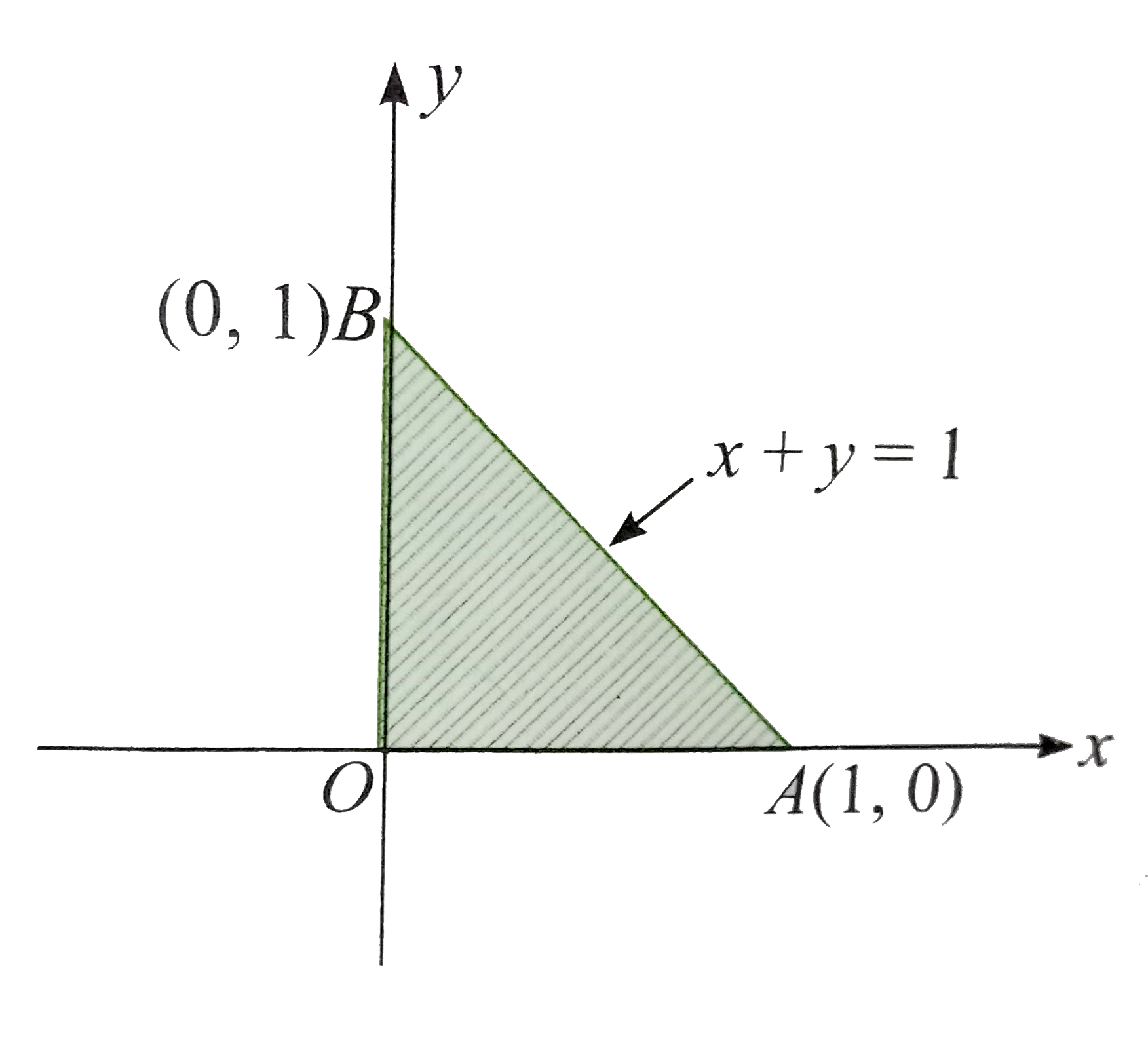
Ifx,y>0, then we have
x+y+x+y≤2 or x+y≤1
These inequalities form a triangle region in the first quadrant formed by axes and lines x+y = 1.
Ifx,y<0, then we have
−x−y−x−y≤2 or x+y≥−1
These inequalities form a triangular region in the third quadrant formed by axes and lines x+y=-1.
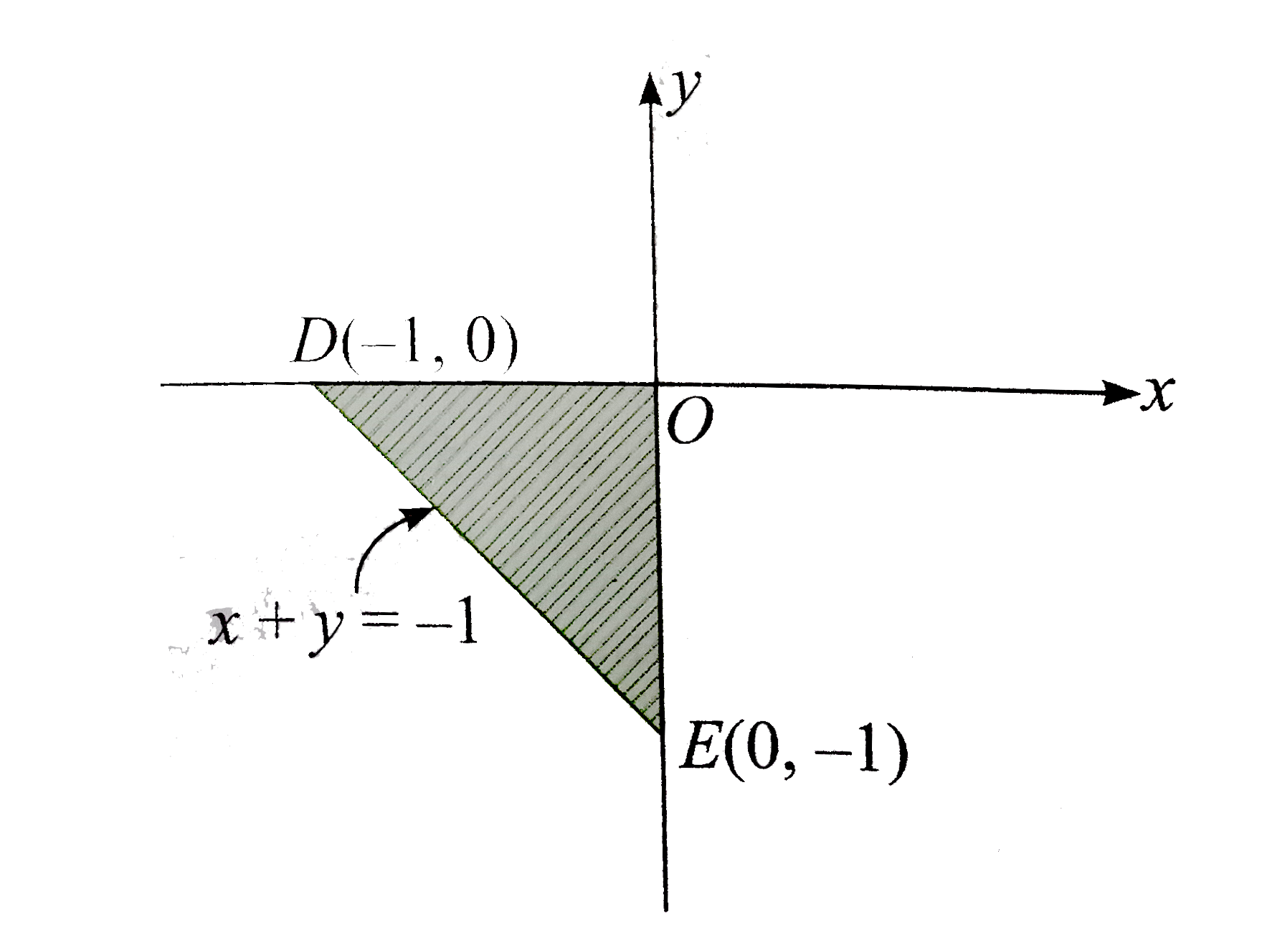
Ifx>0,y<0 and x+y>0, then we have
These inequalities form a triangular region in the fourth quadrant formed by a-axis, a+xy = 0 and x =1.

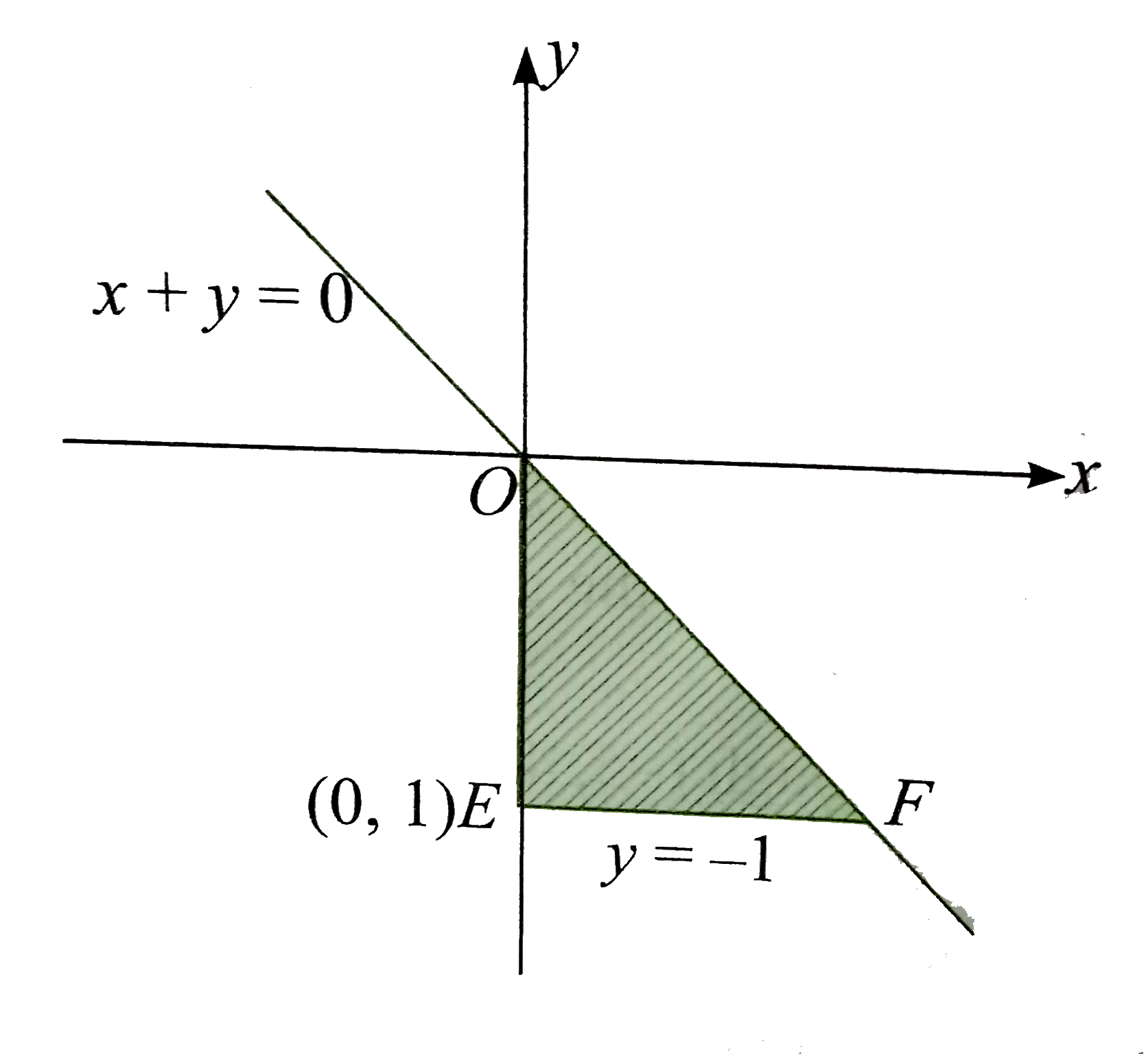
Ifx>0,y<0 and x+y<0, then we have
x−y−x−y≤2 or y≥−1
These inequalities form a trianglular region in the fourth quadrant formed by y-axis, x+y = 0 and y=-1
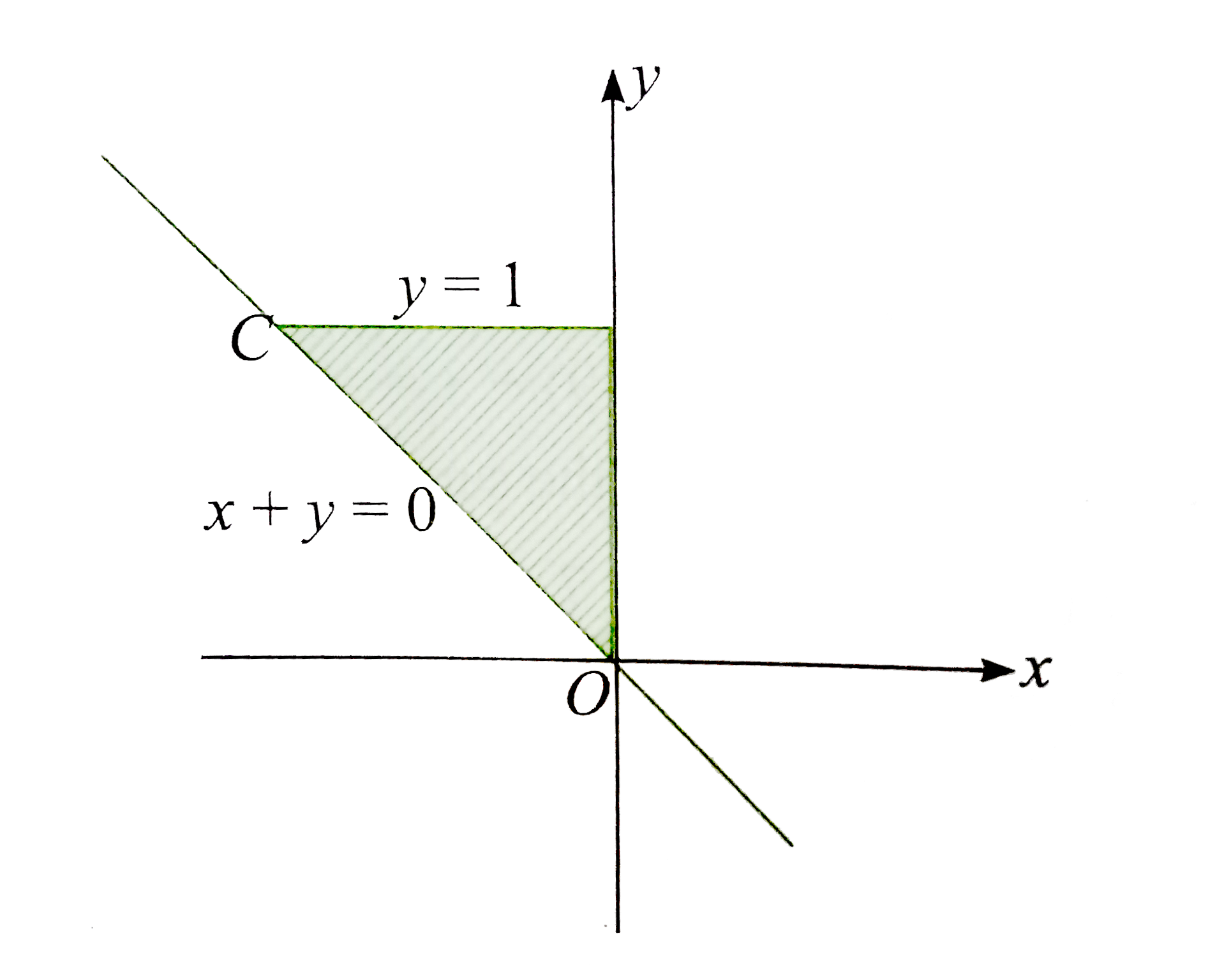
Ifx<0,y>0 and x+y>0, then we have
−x+y+x+y≤2 or y≤1
These inequalities form a triangular region in the second quadrant formed by y-axis, x+y = 0 and y=1.
Ifx<0,y>0 and x+y<0, then we have
−x+y−x−y≤2 or x≥−1
These inequalities form a triangular region in the second quadrant formed by x-axis, x+y=0 and x =-1.
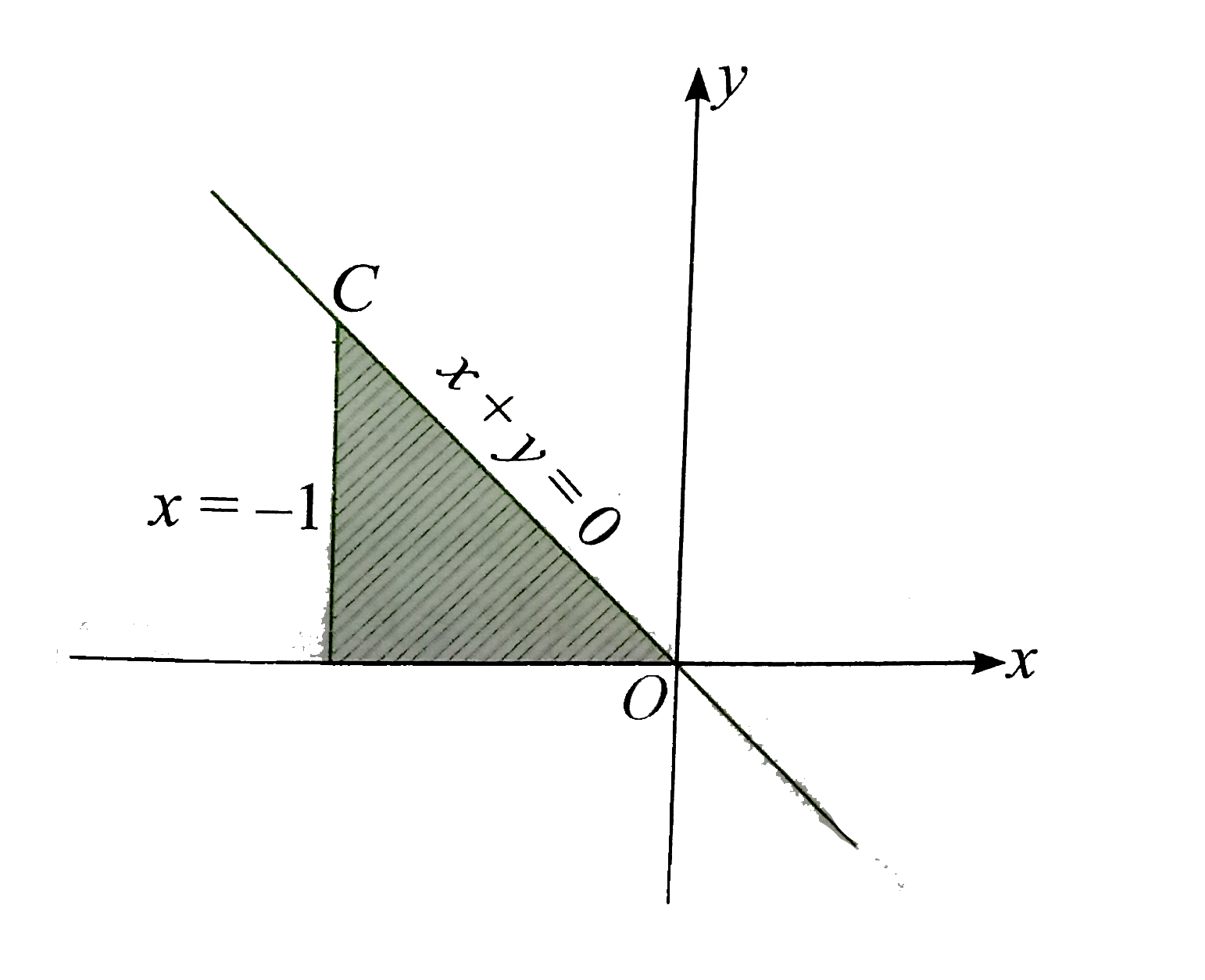
Combining all the regions, we have following region in the plane
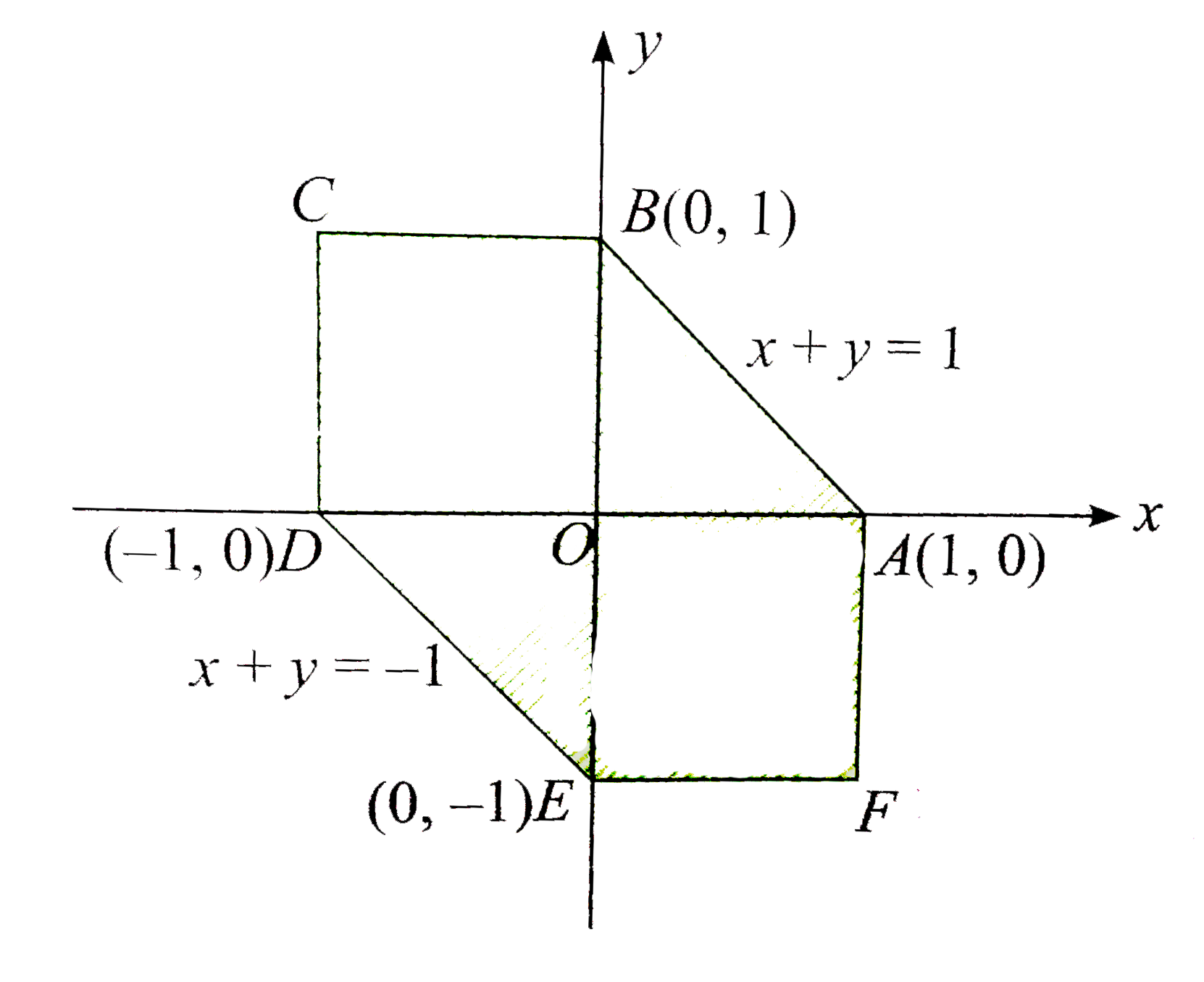
Area of the above region =3× Area of square having side length 1 unit.
= 3 sq. unit.
Topper's Solved these Questions
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:Exercise 2.5
Explore 8 Videos
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:Exercise 2.6
Explore 5 Videos
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:Exercise 2.3
Explore 7 Videos
- STRAIGHT LINEBook:CENGAGEChapter:STRAIGHT LINEExercise:Multiple Correct Answers Type
Explore 8 Videos
- THEORY OF EQUATIONSBook:CENGAGEChapter:THEORY OF EQUATIONSExercise:JEE Advanced Previous Year
Explore 9 Videos
Similar Questions
Find the equation of the bisector of the obtuse angle between the lines 3x−4y+7=0 and 12x+5y−2=0.
View SolutionIf aandb are two arbitrary constants, then prove that the straight line (a−2b)x+(a+3b)y+3a+4b=0 will pass through a fixed point. Find that point.
View SolutionFind the points on y−aξs whose perpendicular distance from the line 4x−3y−12=0 is 3.
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionQ. Let p and q real number such that p≠0,p2≠q and p2≠−q. if α and β are non-zero complex number satisfying α+β=−p and α3+β3=q, then a quadratic equation having αβ and βα as its roots is
View SolutionFind the area of the region {(x,y):0≤y≤x2+1,0≤y≤x+1,0≤x≤2}.
View SolutionThe area of the region described by A = {(x,y) : x^(2)+y^(2) le 1 and y^(2) le 1-x} is :
View SolutionFind the area of the region {(x,y):x2+y2≤2ax , y2≤ax , x≤0 , y≤0}
View SolutionThe area of the region bounded by the curves {(x,y):x2+y2≤4,2≤x+y} is __________ .
View Solutionक्षेत्र {(x,y):0≤y≤x2+1,y≤x+1,0≤x≤2} का क्षेत्रफल ज्ञात कीजिए।
View SolutionThe area defined by 2≤|X+y|+|x−y|≤4 is
View SolutionThe area of the region described by {(x,y)//x^2 + y^2 le 1 and y^2 le 1-x} is
View Solutionक्षेत्र {(x,y):x2≤y≤|x|} का क्षेत्रफल है
View SolutionCalculate the area enclosed in the region
(i) {(x,y):x2+y2≤1≤x+y}
(ii) {(x,y):x2+y2≤4x,4x2+4y2≤9}
(iii) {(x,y):x2+y2≤16,x2≤6y}
(iv) {(x,y):y2≤6ax,x2+y2≤16a2}
(v) {(x,y):x2+y2≤8,x2≤2y}.
View SolutionThe area {(x,y):x2≤y≤√x} is equal to :
View SolutionFind the area of the region {(x,y):0≤y≤x2,0≤y≤x+2,0≤x≤3}.
View Solution
