If the point P(a2,a) lies in the region corresponding to the acute angle between the lines 2y=x and 4y=x , then find the values of a.Solution in Tamil
The correct Answer is:α∈(2,4)
Acute angle is formed by lines in first the third quadrants.
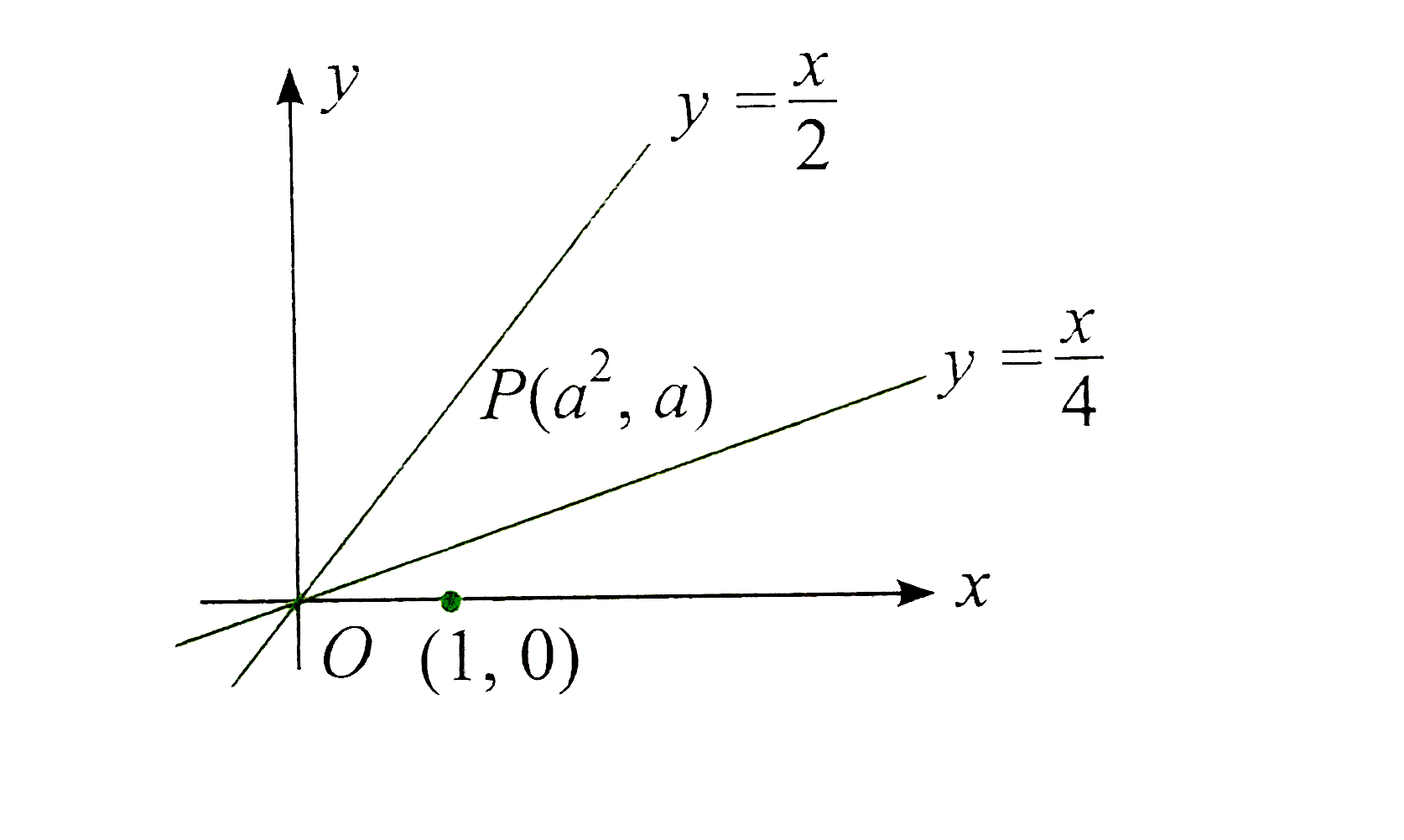
But a2>0, and hence, point P(a2,a) lies in the first quadrant.
We have a−a24>0 and a−a22<0
⇒a∈(0,4) and a∈(−∞,0)∪(2,∞)
⇒a∈(2,4)
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.58videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.65videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.37videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year9videos
THEORY OF EQUATIONS
Similar Questions
Find the equation of the bisector of the obtuse angle between the lines 3x−4y+7=0 and 12x+5y−2=0.
03:15View SolutionIf aandb are two arbitrary constants, then prove that the straight line (a−2b)x+(a+3b)y+3a+4b=0 will pass through a fixed point. Find that point.
04:01View SolutionFind the points on y−aξs whose perpendicular distance from the line 4x−3y−12=0 is 3.
07:46View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
09:10View SolutionQ. Let p and q real number such that p≠0,p2≠q and p2≠−q. if α and β are non-zero complex number satisfying α+β=−p and α3+β3=q, then a quadratic equation having αβ and βα as its roots is
05:30View SolutionIf the point P(a2,a) lies in the region corresponding to the acute angle between the lines 2y=x and 4y=x , then find the values of a.
04:28View SolutionIf the point (1+cos theta,sin theta) lies between the region corresponding to the acute angle between the lines 3y=x and 6y=x, then
05:33View SolutionFind the area of the region between the parabola x=4y-y^(2) and the line x=2y-3
03:57View SolutionIf the point (a,a) is placed in between the lines |x+y|=4, then find the values of a.
03:29View SolutionIf the point P(a2,a) lies in the region corresponding to the acute angle between the lines 2y=x and 4y=x , then find the values of a.
06:25View SolutionIf the point (a2,a+1) lies in the angle between the lines 3x−y+1=0 and x+2y−5=0 containing the origin, then find the value of a.
03:47View SolutionThe acute angle between the line 3x−4y=5 and the circle x2+y2−4x+2y−4=0 is θ . Then find the value of 9cosθ.
03:11View SolutionIf the point (a2,a+1) lies in the angle between the lines 3x−y+1=0 and x+2y−5=0 containing the origin, then find the value of a.
05:00View SolutionIf the point (a,a) is placed in between the lines |x+y|=4, then find the values of a.
05:38View SolutionIf the point P(a2,a) lies in the region corresponding to the acute angle between the lines 2y=x and 4y=x , then find the values of a.
04:24View Solution
