Question

Find the greatest value of $f\left(x\right)\frac{1}{2ax-x^2-5a^2}\in [-3,5]$
depending upon the parameter $a\stackrel{.}{}$

Explanation

We have `f(x)=(1)/(2ax-x^(2)-5a^(2))=(1)/(-4a^(2)-(x-a)^(2))`
Let us first draw the graph of `y=f(x)`.
Clearly, f(x) is continuous `AA x in R`.
`f(0)=(1)/(-5a^(2))`. Hence the graph cuts the y-axis at its negative side.
`f(a-x)=f(a+x)`. Hence the graph is symmetrical about the line x = a.
Clearly, `y=f(x)` is minimum when `x=a,f(a)=(1)/(-4a^(2))`
Also the graph has horizontal asymptote y = 0 (x-axis).
Graph has no vertical or oblique asymptote.
Further `f(x) lt 0, AA x in R`.
From the above information, the graph of `y=f(x)` is as shown in the following figure.

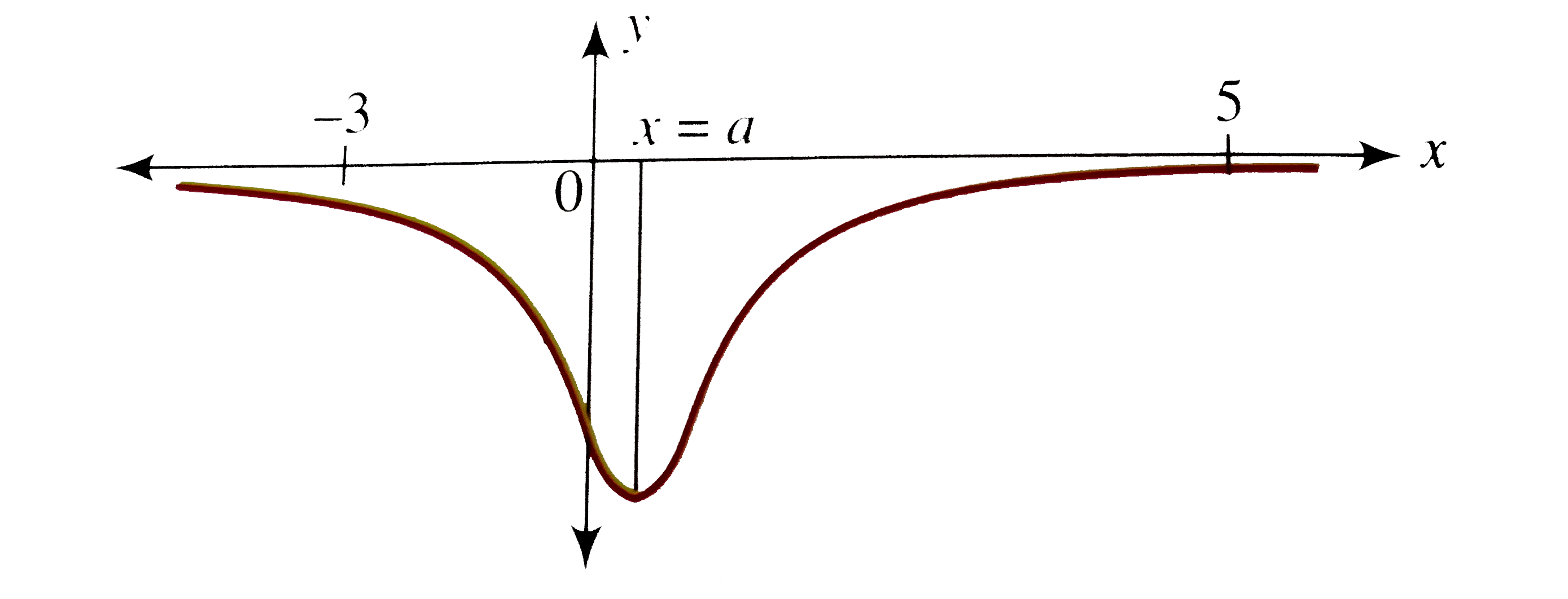
If `a=1` (mid point of`x-3 and x= 5`), the greatest value is `f(5)=f(-3)`.
If `a lt 1, f_("max")(x)=f(5)=(-1)/(5(a^(2)-2a+5))`
and if `agt 1, f_("max")(x)=f(-3)=(-1)/(5a^(2)+6a+9)`