In a group of 50 students, the number of students learning - French, English, Sanskrit were found to be as follows: French = 17, English = 13, Sanskrit = 15, French and English = 09, English and Sanskrit = 4, French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who are learning at?
French only
(ii) English only
(iii) Sanskrit only
(iv) English and Sanskrit but not French
(v) French and Sanskrit but not English
(vi) French and English but not Sanskrit
(vii) at least one of the three languages
(viii) none of the three languages
(ix) exactly one language (X) exactly two languages
 Solution in Tamil
Solution in Tamil

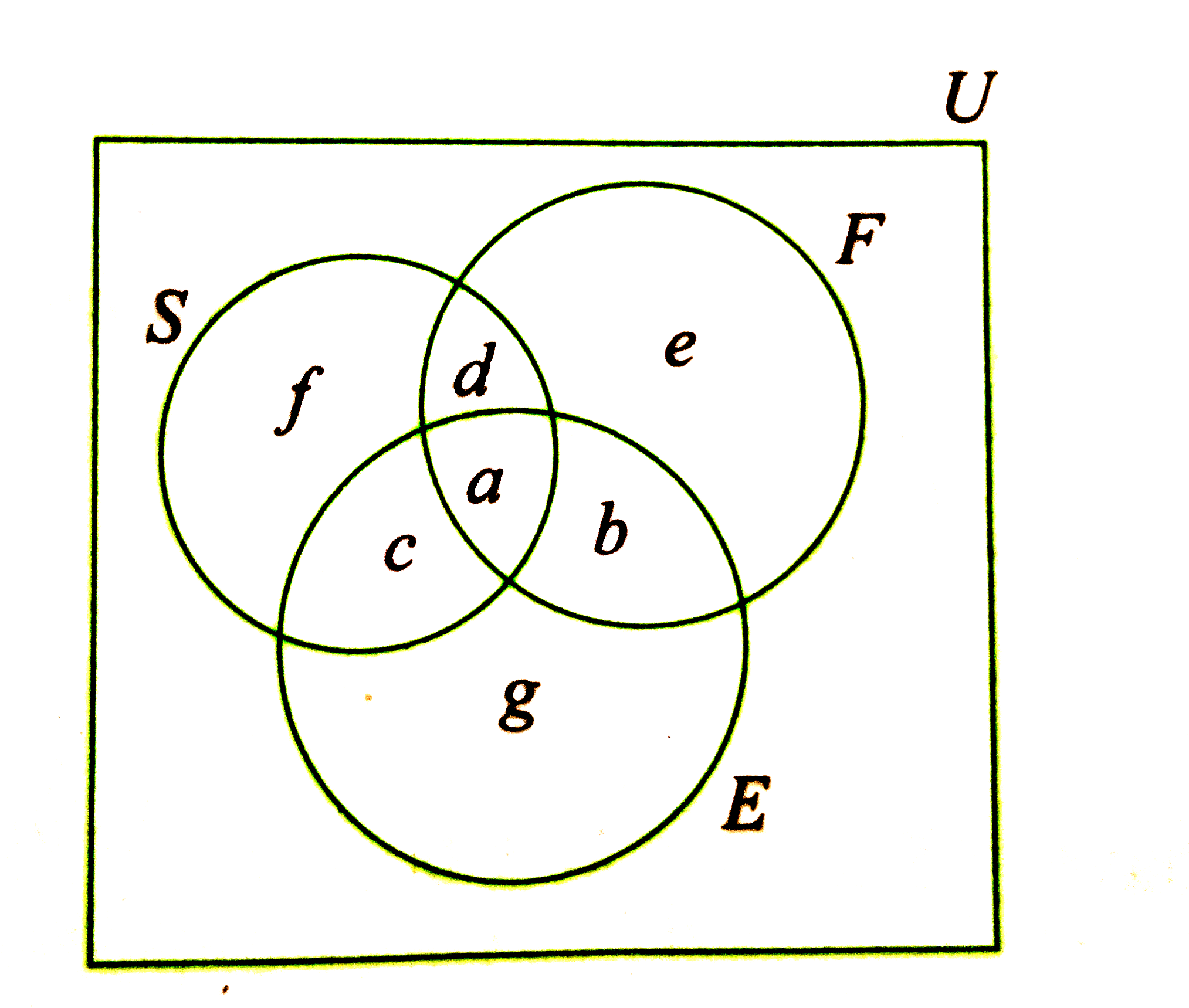
Let pet F, E and S be the sets of students whole arn French, English ,md Sanskrit, respectively. Then,n(U)=50,n(F)=17,n(E)=13,n(S)=15,n(F∩E)=9,n(E∩S)=4,n(F∩S)=5, and n(F∩E∩S)=3. From the figure, we have
a=n(E∩F∩S)=3anda+d=n(F∩S)=5⇒d=2
a+b=n(F∩E)=9⇒b=6
a+c=n(F∩S)=4⇒c=1
a+b+d+e=n(F)=17⇒3+6+2+e=17⇒e=6
a+b+c+g=n(F)=13⇒3+6+1+g=13⇒g=3
a+c+d+f=n(S)=15⇒3+1+2+f=15⇒f=9
Number of student learining French only = e = 6
(ii) Number of students learning English only = g = 3
(iii) Number of students learning Sanskrit only = f = 9
(iv) Number of students learning English and Sanskrit but not French = c = 1
(v) Number of students learning French and Sanskrit but not English = d = 2
(vi) Number of students learning F rench and English but not Sanskrit = b = 6
(vii) Number of students learning at least one of the three languages=a+b+c+d+e+f+g=30
(viii) Number of students learning none of the three languages = 50 - 30 = 20 .
(ix) Number of students learning exactly one language =e+f+g=6+3+9=18
(x) Number of students learning exactly two languages =b+c+d=6+2+l=9
Topper's Solved these Questions
- SET THEORY AND REAL NUMBER SYSTEM BOOK - CENGAGECHAPTER - SET THEORY AND REAL NUMBER SYSTEM EXERCISE - Exercise 1.1
12 Videos
- SET THEORY AND REAL NUMBER SYSTEM BOOK - CENGAGECHAPTER - SET THEORY AND REAL NUMBER SYSTEM EXERCISE - Exercise 1.2
8 Videos
- SEQUENCE AND SERIESBOOK - CENGAGECHAPTER - SEQUENCE AND SERIESEXERCISE - Question Bank
1 Videos
- SETS AND RELATIONSBOOK - CENGAGECHAPTER - SETS AND RELATIONSEXERCISE - Question Bank
3 Videos
Similar Questions
Examine whether A= { x:x is a positive integer divisible by 3} is a subset of B= { x:x is a multiple of 5, x∈N }.
View SolutionFind the values of x which satisfy the following inequalities simultaneously:
(a) −3<2x−1<19
(b ) −1≤2x+35≤3
View SolutionLet a,b,c∈R+ and 2ab3+a2b3+b3=243 . If 2a+3b+2 assumes its least value, then a+b is equal to
View SolutionLet n(U)=700, n(A)=200, n(B)=300 and n(A∩B)=100, then n(Ac∩Bc)=
View SolutionIn a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows French = 17, English = 13, Sanskrit = 15 French and English = 09, English and Sanskrit = 4, French and Sanskrit = 5, English , French and Sanskrit = 3. Find the number of students who study
(i) only French, (ii) only English.
(iii) only Sanskrit. , (iv) English and Sanskrit but not French.
(v) French and Sanskrit but not English.
(vi) French and English but not Sanskrit.
(vii) atleast one of the three languages.
(viii) none of the three languages.
View SolutionIn a group of 50 students, the number of students learning - French, English, Sanskrit were found to be as follows: French = 17, English = 13, Sanskrit = 15, French and English = 09, English and Sanskrit = 4, French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who are learning at?
French only
(ii) English only
(iii) Sanskrit only
(iv) English and Sanskrit but not French
(v) French and Sanskrit but not English
(vi) French and English but not Sanskrit
(vii) at least one of the three languages
(viii) none of the three languages
(ix) exactly one language (X) exactly two languages

View SolutionThe students of a class are offered three languages (Hindi, English and French). 15 students learn all the three languages whereas 28 students do not learn any language. The number of students learning Hindi and English but not French is twice the number of students learning Hindi French but not English. The number of students learning English and French but not Hindi is thrice the number of students learning Hindi and French but not English. 23 students learn only Hindi and 17 students learn only English. The total number of students learning French is 46 and the total number of students learning only French is 11.
How many students learn precisely two languages?
View SolutionThe students of a class are offered three languages (Hindi, English and French). 15 students learn all the three languages whereas 28 students do not learn any language. The number of students learning Hindi and English but not French is twice the number of students learning Hindi French but not English. The number of students learning English and French but not Hindi is thrice the number of students learning Hindi and French but not English. 23 students learn only Hindi and 17 students learn only English. The total number of students learning French is 46 and the total number of students learning only French is 11.
How many students learn at least two languages?
View SolutionThe students of a class are offered three languages (Hindi, English and French). 15 students learn all the three languages whereas 28 students do not learn any language. The number of students learning Hindi and English but not French is twice the number of students learning Hindi French but not English. The number of students learning English and French but not Hindi is thrice the number of students learning Hindi and French but not English. 23 students learn only Hindi and 17 students learn only English. The total number of students learning French is 46 and the total number of students learning only French is 11.
How many students learn at least one languages?
View Solution50 विद्यार्थियों के समूह में फ्रेंच, अंग्रेजी तथा संस्कृत पढ़ने वाले विद्यार्थियों की संख्या निम्न है
फ्रेंच = 17, अंग्रेजी = 13, संस्कृत = 15
फ्रेंच तथा अंग्रेजी = 09, अंग्रेजी तथा संस्कृत = 4
फ्रेंच तथा संस्कृत = 5, अंग्रेजी, फ्रेंच तथा संस्कृत = 3
निम्न में से सत्य है
View SolutionIn a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows French = 17, English = 13, Sanskrit = 15 French and English = 09, English and Sanskrit = 4, French and Sanskrit = 5, English , French and Sanskrit = 3. Find the number of students who study
(i) only French, (ii) only English.
(iii) only Sanskrit. , (iv) English and Sanskrit but not French.
(v) French and Sanskrit but not English.
(vi) French and English but not Sanskrit.
(vii) atleast one of the three languages.
(viii) none of the three languages.
View SolutionIn a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows French = 17, English = 13, Sanskrit = 15, French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study
Only French.
View SolutionIn a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows French = 17, English = 13, Sanskrit = 15, French and English = 9, English and Sanskrit =4 , French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study
Only English.
View SolutionIn a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows French = 17, English = 13, Sanskrit = 15, French and English = 9, English and Sanskrit = 4, French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study
Only Sanskrit.
View SolutionIn a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows French = 17, English = 13, Sanskrit = 15, French and English = 9, English and Sanskrit = 4 French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study
English and Sanskrit but not French.
View Solution
