Question

In a group of 50 students, the number of students learning - French, English, Sanskrit were found to be as follows: French = 17, English = 13, Sanskrit = 15, French and English = 09, English and Sanskrit = 4, French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who are learning at?
French only
(ii) English only
(iii) Sanskrit only
(iv) English and Sanskrit but not French
(v) French and Sanskrit but not English
(vi) French and English but not Sanskrit
(vii) at least one of the three languages
(viii) none of the three languages
(ix) exactly one language (X) exactly two languages

Explanation

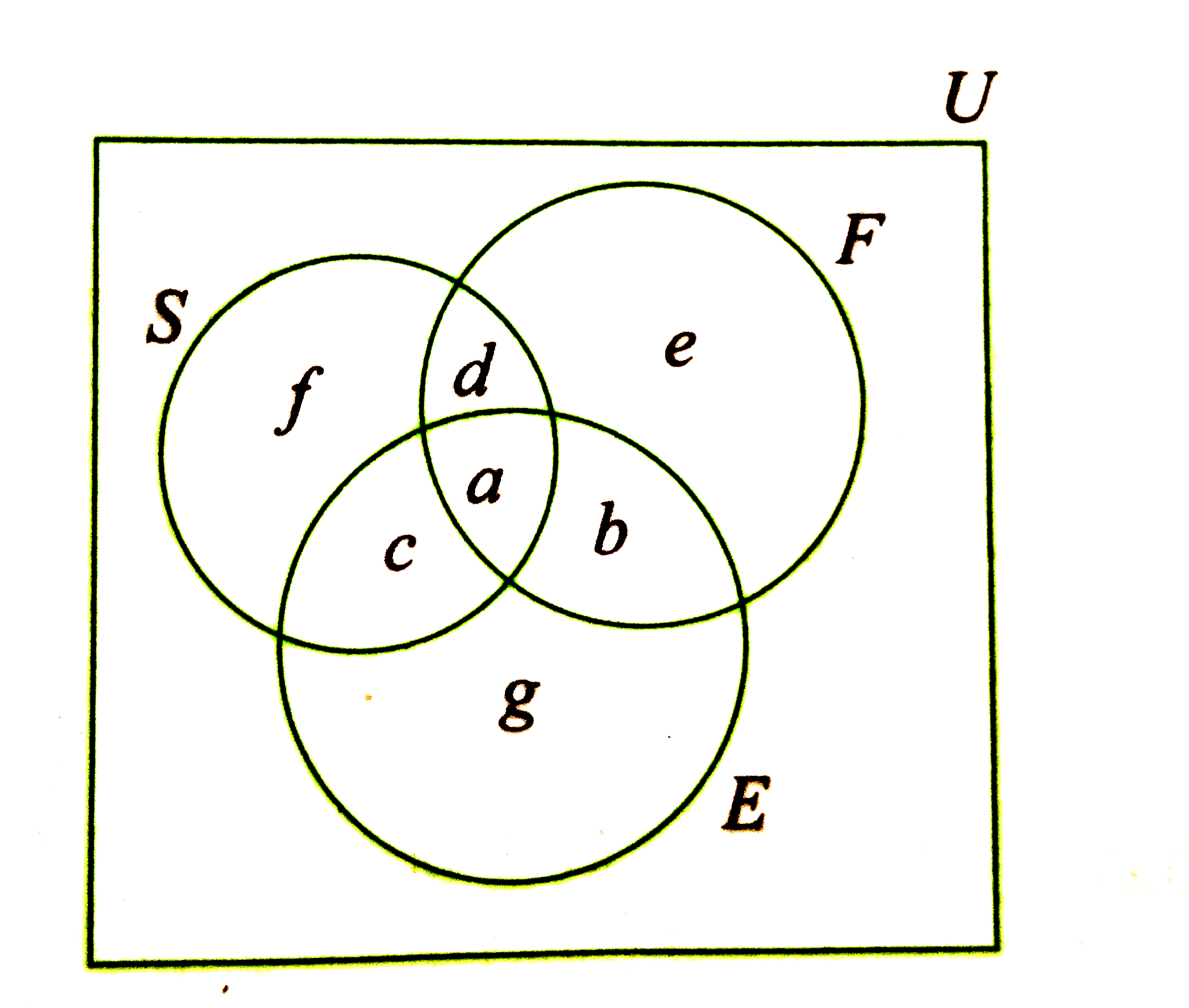
Let pet F, E and S be the sets of students whole arn French, English ,md Sanskrit, respectively. Then,` n(U) = 50, n(F) = 17, n(E)=13, n(S) = 15, n(F cap E)=9,n(E cap S)=4,n(F cap S)=5," and " n(F cap E cap S)=3`. From the figure, we have
`a= n ( E cap F cap S )=3 and a+d =n ( F cap S) = 5 rArr d= 2 `
`a + b =n ( F cap E )= 9 rArr b=6 `
`a+ c =n ( F cap S )=4 rArr c= 1`
`a+b+d+e = n ( F) = 17 rArr 3+ 6+ 2+ e= 17 rArr e= 6`
`a+b+c+g = n ( F) = 13 rArr 3+6+1+g= 13 rArr g=3`
`a+c+d+f =n (S) = 15 rArr 3+1+2+f = 15 rArr f=9 `
Number of student learining French only = e = 6
(ii) Number of students learning English only = g = 3
(iii) Number of students learning Sanskrit only = f = 9
(iv) Number of students learning English and Sanskrit but not French = c = 1
(v) Number of students learning French and Sanskrit but not English = d = 2
(vi) Number of students learning F rench and English but not Sanskrit = b = 6
(vii) Number of students learning at least one of the three languages=a+b+c+d+e+f+g=30
(viii) Number of students learning none of the three languages = 50 - 30 = 20 .
(ix) Number of students learning exactly one language =e+f+g=6+3+9=18
(x) Number of students learning exactly two languages =b+c+d=6+2+l=9