Consider triangle in the plane, where The new position of when triangle is rotated about side by can be Solution in Tamil
The correct Answer is:c
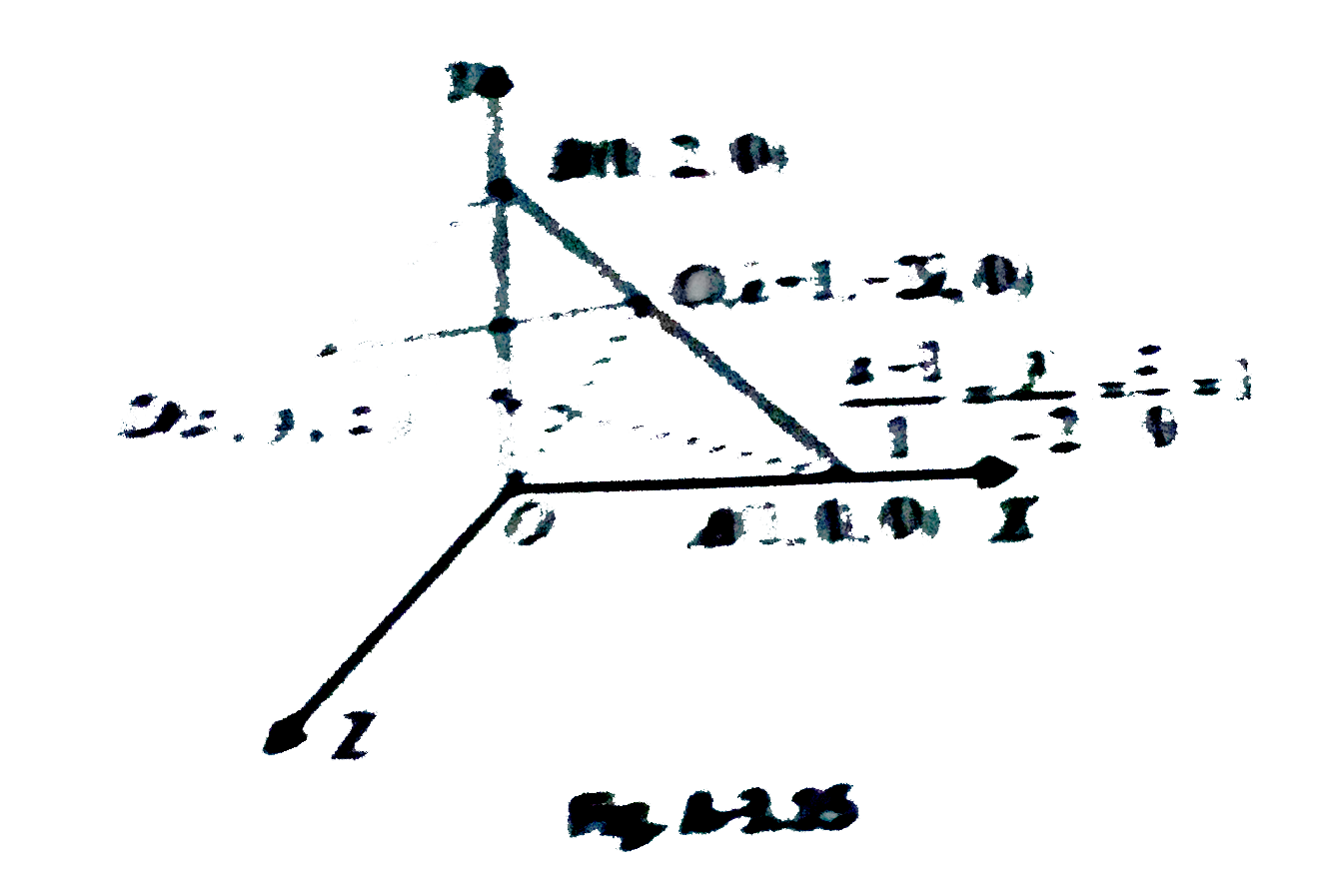
Equation of line is
Now
or
is . Now
(i)
and (ii)
Now
(iii)
From (i) and (ii), we get
From (iii), putting . Putting this value of in (i), we get
Topper's Solved these Questions
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise (Multiple)
17 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise (Reasoning Questions)
10 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - SUBJECTIVE TYPE
1 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGECHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Question Bank
12 Videos
- TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONSBOOK - CENGAGECHAPTER - TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONSEXERCISE - Question Bank
4 Videos
Similar Questions
Let PM be the perpendicular from the point P(1,2,3) to the x−y plane. If →OP makes an angle θ with the positive direction of the z− axis and→OM makes an angle φ with the positive direction of x− axis, whereO is the origin and θandφ are acute angels, then a. cosθcosφ=1/√14 b. sinθsinφ=2/√14 c. tanφ=2 d. tanθ=√5/3
View SolutionStatement 1 : Lines →r=ˆi−ˆj+λ(ˆi+ˆj−ˆk)and→r=2ˆi−ˆj+μ(ˆi+ˆj−ˆk) do not intersect.
Statement 2 : Skew lines never intersect.
View SolutionProve that the volume of tetrahedron bounded by the planes →r.mˆj+nˆk=0,→r.nˆk+lˆi=0,→r.lˆi+mˆj=0,→r.lˆi+mˆj+nˆk=πs2p33lmn
View SolutionThe equation of the plane which has the property that the point Q(5,4,5) is the reflection of point P(1,2,3) through that plane, is ax+by+cz=d where a,b,c,d∈N. Find the least value of (a+b+c+d).
View SolutionThe number of solution (s) of the equation
√2+cos2x=(sinx+cosx)∈[−π2,π]
View SolutionIf O is a point in space, ABC is a triangle and D,E,F are the mid-points of the sides BC,CA and AB respectively of the triangle, prove that →OA + →OB+→OC=→OD+→OE+→OF.
View SolutionConsider triangle AOB in the x−y plane, where A≡(1,0,0),B≡(0,2,0)andO≡(0,0,0). The new position of O, when triangle is rotated about side AB by 900 can be a. (45,35,2√5) b. (−35,√25,2√5) c. (45,25,2√5) d. (45,25,1√5)
View Solutionनिम्नलिखित में किसका व्युत्क्रम ज्ञात किया जा सकता है ?
(a ) ⎡⎢⎣100020000⎤⎥⎦
(b )⎡⎢⎣100020003⎤⎥⎦
View SolutionConsider the triangle OAB where O(0,0),B(3,4) ,if the orthocentre of a triangle is H(1,4) and co-ordinates of A is (a,b) ,then a+b
View SolutionConsider triangle AOB in the x−y plane, where A≡(1,0,0),B≡(0,2,0)andO≡(0,0,0). The new position of O, when triangle is rotated about side AB by 900 can be a. (45,35,2√5) b. (−35,√25,2√5) c. (45,25,2√5) d. (45,25,1√5)
View SolutionConsider triangle AOB in the x−y plane, where A≡(1,0,0),B≡(0,2,0)andO≡(0,0,0). The new position of O, when triangle is rotated about side AB by 900 can be a. (45,35,2√5) b. (−35,√25,2√5) c. (45,25,2√5) d. (45,25,1√5)
View SolutionIf O is a point in space, ABC is a triangle and D,E,F are the mid-points of the sides BC,CA and AB respectively of the triangle, prove that →OA + →OB+→OC=→OD+→OE+→OF.
View SolutionIn a △ ABC, If L and M are points on AB and AC respectively such that LM∣∣BC. Prove that: ar (△ LOB)=ar (△ MOC)
View SolutionO is any point on the diagonal BD of the parallelogram ABCD. Prove that ar(△OAB)=ar(△OBC)
View SolutionThe bisects of exterior angles at B and C of triangle ABC meet at O. If A=x∘, then BOC=
(a)900+x02
(b) 900−x02
(c)1800+x02
(d) 1800−x02
View SolutionIf O is a point in space, ABC is a triangle and D,E,F are the mid-points of the sides BC,CA and AB respectively of the triangle, prove that →OA + →OB+→OC=→OD+→OE+→OF.
View Solution
