Question

Consider triangle $AOB$
in the $x-y$
plane, where $A\equiv (1,0,0),B\equiv (0,2,0)andO\equiv (0,0,0)\stackrel{.}{}$
The new position of $O,$
when triangle is rotated about side $AB$
by ${90}^0$
can be
a. $(\frac{4}{5},\frac{3}{5},\frac{2}{\sqrt{5}})$
b. $(\frac{-3}{5},\frac{\sqrt{2}}{5},\frac{2}{\sqrt{5}})$

c. $(\frac{4}{5},\frac{2}{5},\frac{2}{\sqrt{5}})$
d. $(\frac{4}{5},\frac{2}{5},\frac{1}{\sqrt{5}})$

Options

A. `((4)/(5),(3)/(5),(2)/(sqrt5))`
B. `((-3)/(5),(sqrt2)/(5),(2)/(sqrt5))`
C. `((4)/(5),(2)/(5),(2)/(sqrt5))`
D. `((4)/(5),(2)/(5),(1)/(sqrt5))`

Answer

c

Explanation

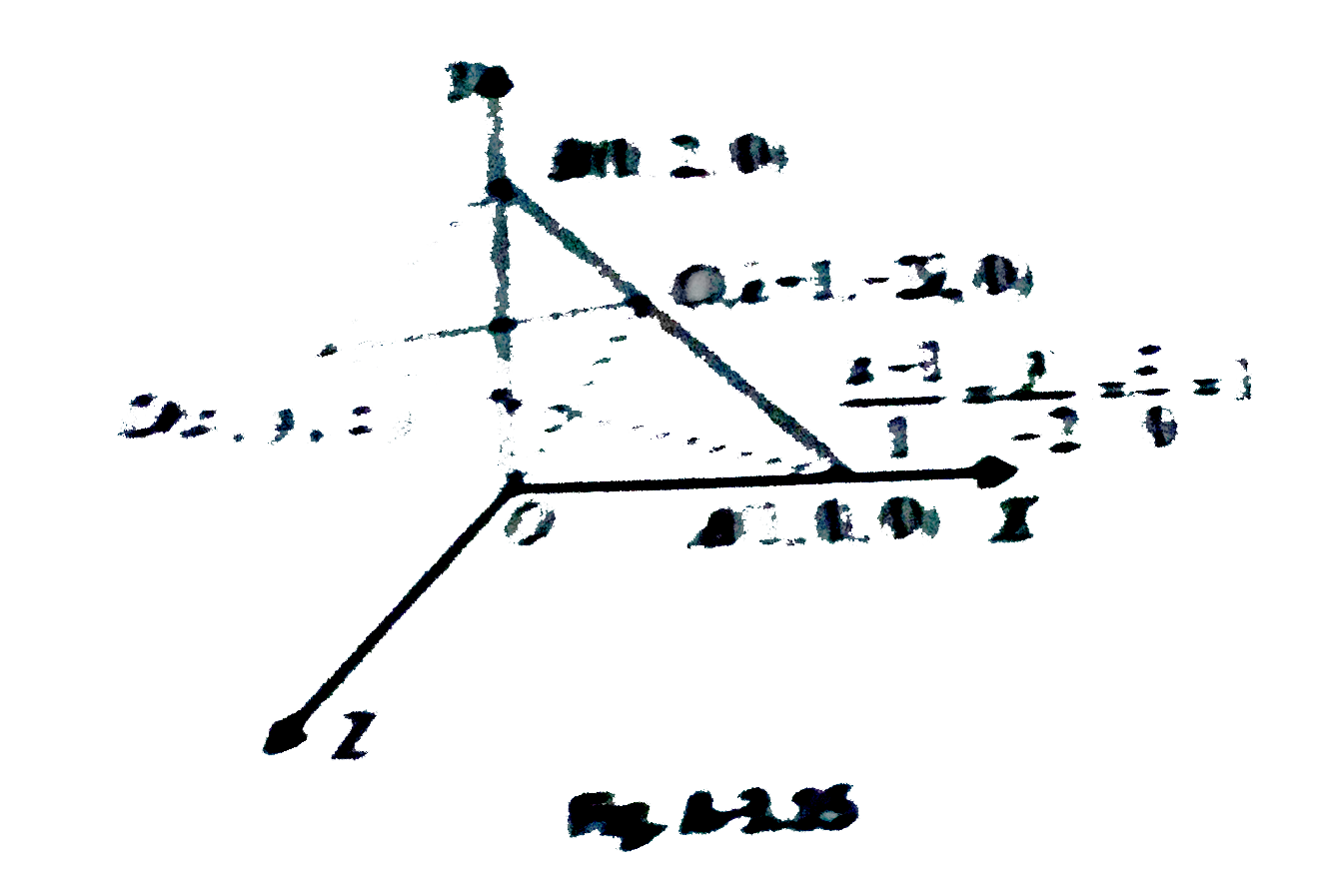
Equation of line `AB` is `(x-1)/(1)= (y)/(-2) = (z)/(0) = lamda`
Now `AB bot OC rArr 1 (lamda+1)+ (-2lamda)(-2)=0`
or `" "5lamda=-1 or lamda=-(1)/(5)`
`rArr" "C` is `((4)/(5), (2)/(5), 0)`. Now
`" "x_(1)^(2)+ (y_(1)-2)^(2)+ z_(1)^(2)= 4" "`(i)
and `" "(x_(1)-1)^(2)+ y_(1)^(2)+ z_(1)^(2)= 1" "`(ii)
Now `OC bot CD`
`rArr" "(x_(1)- (4)/(5))(4)/(5) + (y_(1)- (2)/(5)) (2)/(5) + (z_(1)-0 ) 0=0" "` (iii)
From (i) and (ii), we get
`" "-4y_(1)+ 2x_(1)=0 or x_(1) = 2y_(1)`
From (iii), putting `x_(1)= 2y_(1) rArr 2y_(1) =(4)/(5) or y_(1) = (2)/(5) rArr x_1= (4)(5)`. Putting this value of `x_1 and y_1` in (i), we get
`" "z_(1)= pm (2)/(sqrt5)`