The distance of point A(−2,3,1) from the line PQ through P(−3,5,2), which makes equal angles with the axes is a. 2/√3 b. 14/√3 c. 16/√3 d. 5/√3Solution in Tamil
2/√3
√14/3
16/√3
5/√3
The correct Answer is:B
Here, α=β=γ
∵cos2α+cos2β+cos2γ=1
∵cosα=1√3
Direction cosines of PQ are (1√3,1√3,1√3)
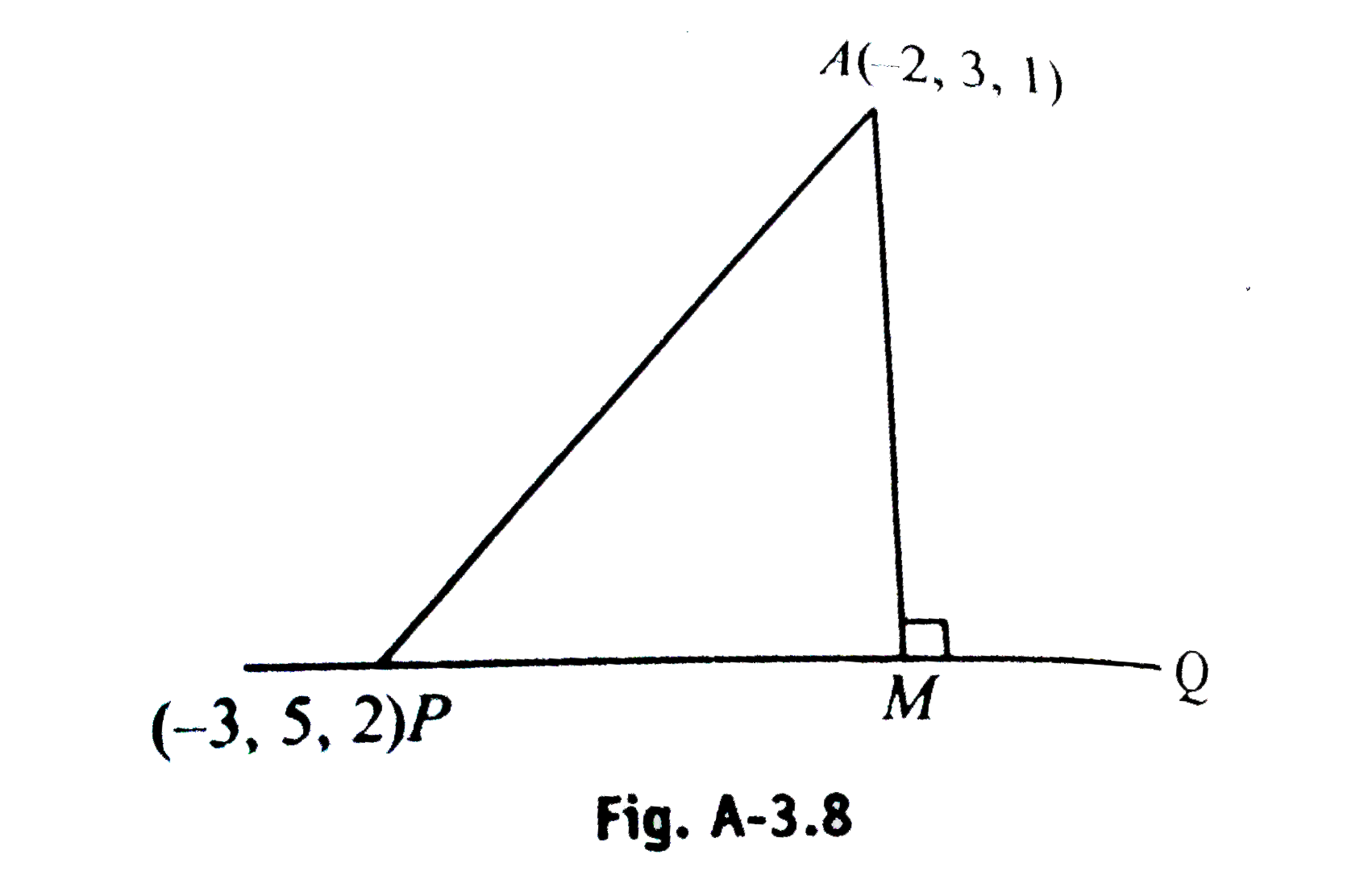
PM=Projection of AP on PQ
=∣∣∣(−2+3)1√3+(3−5)1√3+(1−2)1√3∣∣∣
=2√3
and AP=√(−2+3)2+(3−5)2+(1−2)2=√6
AM=√(AP)2−(PM)2=√6−43=√143
Topper's Solved these Questions
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise (Multiple)
17 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise (Reasoning Questions)
10 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - SUBJECTIVE TYPE
1 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGECHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Question Bank
12 Videos
- TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONSBOOK - CENGAGECHAPTER - TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONSEXERCISE - Question Bank
4 Videos
Similar Questions
Let PM be the perpendicular from the point P(1,2,3) to the x−y plane. If →OP makes an angle θ with the positive direction of the z− axis and→OM makes an angle φ with the positive direction of x− axis, whereO is the origin and θandφ are acute angels, then a. cosθcosφ=1/√14 b. sinθsinφ=2/√14 c. tanφ=2 d. tanθ=√5/3
View SolutionStatement 1 : Lines →r=ˆi−ˆj+λ(ˆi+ˆj−ˆk)and→r=2ˆi−ˆj+μ(ˆi+ˆj−ˆk) do not intersect.
Statement 2 : Skew lines never intersect.
View SolutionProve that the volume of tetrahedron bounded by the planes →r.mˆj+nˆk=0,→r.nˆk+lˆi=0,→r.lˆi+mˆj=0,→r.lˆi+mˆj+nˆk=πs2p33lmn
View SolutionThe equation of the plane which has the property that the point Q(5,4,5) is the reflection of point P(1,2,3) through that plane, is ax+by+cz=d where a,b,c,d∈N. Find the least value of (a+b+c+d).
View SolutionThe number of solution (s) of the equation
√2+cos2x=(sinx+cosx)∈[−π2,π]
View SolutionIf the axes are rotated through 30^(@) in the anti- clockwise direction,the coordinates of points (4,-2sqrt(3)) with respect to new axes are (A)(2,sqrt(3)) (B) (sqrt(3),-5) (C) (2,3) (D) ( sqrt(3),2)
View SolutionA hyperbola passes through the point P(sqrt(2),sqrt(3)) and has foci at (+-2,0) them the tangent to this hyperbola at P also passes through the point (A)(sqrt(3),sqrt(2))(B)(-sqrt(2),-sqrt(3))(C)(3sqrt(2),2sqrt(3))(D)(2sqrt(2),3sqrt(3))
View SolutionThe distance of point A(−2,3,1) from the line PQ through P(−3,5,2), which makes equal angles with the axes is a. 2/√3 b. 14/√3 c. 16/√3 d. 5/√3
View SolutionIf P+sqrt(3)Q+sqrt(5)R+sqrt(15)S=(1)/(1+sqrt(3)+sqrt(5)) then the value of P is
View SolutionIf x=√5+√3√5−√3 and y=√5−√3√5+√3, then (x+y) equals (a) 2(√5+√3) (b) 2√15 (c) 8 (d) 16
View SolutionIf p=3−√53+√5andq=3+√53−√5,find the value of p2+q2.
View SolutionP and Q are points on the line joining A(−2,5) and B(3,1) such that AP=PQ=QB . Then the distance of the midpoint of PQ from the origin is (a)3 (b) √372 (c) 4 (d) 3.5
View SolutionIf tangents PQ and PR are drawn from a point on the circle x2+y2=25 to the ellipse x216+y2b2=1,(b<4), so that the fourth vertex S of parallelogram PQSR lies on the circumcircle of triangle PQR , then the eccentricity of the ellipse is
(a)√54
(b) √74
(c) √72
(d) √53
View SolutionThe distance of point A(−2,3,1) from the line PQ through P(−3,5,2), which makes equal angles with the axes is a. 2/√3 b. √14/3 c. 16/√3 d. 5/√3
View SolutionThe distance of point A(−2,3,1) from the line PQ through P(−3,5,2), which makes equal angles with the axes is
View SolutionThe distance of point A(-2,3,1)from the line PQ through P( 3,5,2), which make equal angles with the axes is
View Solution
