The coordinates o the foot of the perpendicular drawn from the origin to the line joining the point (−9,4,5)and(10,0,−1) will be a. (−3,2,1) b. (1,2,2) c. 4,5,3 d. none of theseSolution in Tamil
(-3,2,1)
(1,2,2,)
(4,5,3)
none of these
The correct Answer is:D
Let AD be the perpendicular and D be the foot of the perpendicular which divides BC in the ratio λ:1, then
D(10λ−9λ+1,4λ+1,−λ+5λ+1) (i)
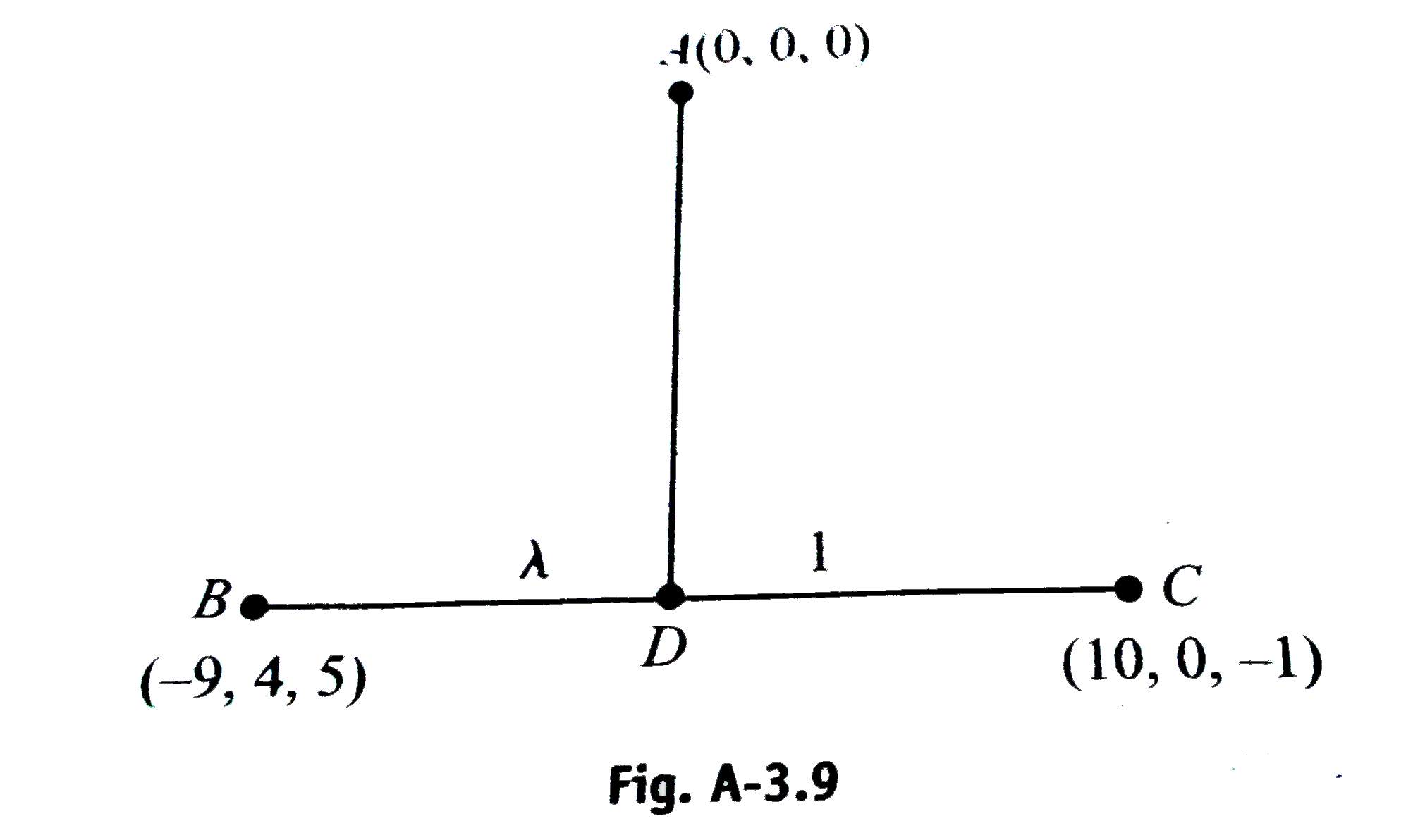
The direction ratio of AD are 10λ−0λ+1,4λ+1and−λ+5λ+1 and direction ratios of BC are 19,-4 and -6.
Since AD⊥BC, we get
19(10λ−9λ+1)−4(4λ+1)−6(−λ+5λ+1)=0
or λ=3128
Hence, on putting the value of λ in (i) ,we get required foot of the perpendicular, i.e., (5859,11259,10959).
Topper's Solved these Questions
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise (Multiple)
17 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise (Reasoning Questions)
10 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - SUBJECTIVE TYPE
1 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGECHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Question Bank
12 Videos
- TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONSBOOK - CENGAGECHAPTER - TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONSEXERCISE - Question Bank
4 Videos
Similar Questions
Let PM be the perpendicular from the point P(1,2,3) to the x−y plane. If →OP makes an angle θ with the positive direction of the z− axis and→OM makes an angle φ with the positive direction of x− axis, whereO is the origin and θandφ are acute angels, then a. cosθcosφ=1/√14 b. sinθsinφ=2/√14 c. tanφ=2 d. tanθ=√5/3
View SolutionStatement 1 : Lines →r=ˆi−ˆj+λ(ˆi+ˆj−ˆk)and→r=2ˆi−ˆj+μ(ˆi+ˆj−ˆk) do not intersect.
Statement 2 : Skew lines never intersect.
View SolutionProve that the volume of tetrahedron bounded by the planes →r.mˆj+nˆk=0,→r.nˆk+lˆi=0,→r.lˆi+mˆj=0,→r.lˆi+mˆj+nˆk=πs2p33lmn
View SolutionThe equation of the plane which has the property that the point Q(5,4,5) is the reflection of point P(1,2,3) through that plane, is ax+by+cz=d where a,b,c,d∈N. Find the least value of (a+b+c+d).
View SolutionThe number of solution (s) of the equation
√2+cos2x=(sinx+cosx)∈[−π2,π]
View SolutionFind the coordinates of the foot of the perpendicular drawn from the point A(1,2,1) to the line joining B(1,4,6)andC(5,4,4).
View SolutionFind the coordinates of the foot of perpendicular drawn from th point A(1,8,4) to the line joining the points B(0,−1,3)and C(2−3,−1).
View SolutionThe coordinates o the foot of the perpendicular drawn from the origin to the line joining the point (−9,4,5)and(10,0,−1) will be a. (−3,2,1) b. (1,2,2) c. 4,5,3 d. none of these
View SolutionFind the coordinates of the foot of the perpendicular drawn from the point A(1,8,4) to the line joining the points B(0,-1,3) and C(2,-3,-1)
View SolutionThe point in which the join of (-9,4,5) and (11,0,-1) is met by the perpendicular from the origin is-
View Solutionबिंदुओं (-9,4,5) व (10,0,-1) को मिलाने वाली रेखा पर मूलबिंदु से डाले गए लम्ब के पाद बिंदु के निर्देशांक हैं
View SolutionFind the coordinates of the foot of perpendicular drawn from th point A(1,8,4) to the line joining the points B(0,−1,3)andC(2−3,−1).
View SolutionFind the coordinates of the foot of the perpendicular drawn from point A(1,0,3) to the join of points B(4,7,1)andC(3,5,3).
View SolutionThe coordinates o the foot of the perpendicular drawn from the origin to the line joining the point (−9,4,5)and(10,0,−1) will be a. (−3,2,1) b. (1,2,2) c. 4,5,3 d. none of these
View SolutionFind the coordinates of the foot of the perpendicular drawn from point A(1,0,3) to the join of points B(4,7,1)andC(3,5,3).
View SolutionThe coordinates of the foot of the perpendicular drawn from the origin to the line joining the point (−9,4,5) and (10,0,−1) will be
View Solution
