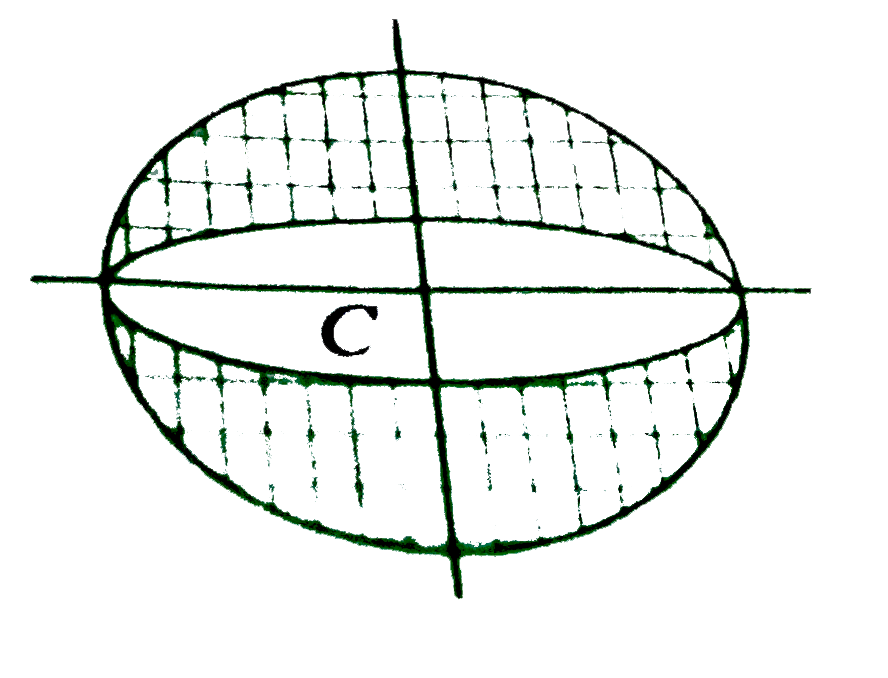
There are some experiment in which the outcomes cannot be identified discretely. For example, an ellipse of eccentricity 2√2/3 is inscribed in a circle and a point within the circle is chosen at random. Now, we want to find the probability that this point lies outside the ellipse. Then, the point must lie in the shaded region shown in Figure. Let the radius of the circle be a and length of minor axis of the ellipse be 2b. Given that
1−b2a2=89orb2a2=19
Then, the area of circle serves as sample space and area of the shaded region represents the area for favorable cases. Then, required probability is
p=Area of shaded regionArea of circle
=πa2−πabπa2=1−ba=1−13=23
Now, answer the following questions.
A point is selected at random inside a circle. The probability that the point is closer to the center of the circle than to its circumference is Solution in Tamil
1/4
1/2
1/3
1/√2
The correct Answer is:A
For the favorable cases, the points should lie inside the concentric circle of radius r/2. So the desired probability is given by

Area of smaller circleArea of larger circle=.π(r2)2πr2=14
Topper's Solved these Questions
- PROBABILITY I BOOK - CENGAGECHAPTER - PROBABILITY I EXERCISE - Exercise (Matrix)
2 Videos
- PROBABILITY I BOOK - CENGAGECHAPTER - PROBABILITY I EXERCISE - Exercise (Numerical)
7 Videos
- PROBABILITY I BOOK - CENGAGECHAPTER - PROBABILITY I EXERCISE - Exercise (Multiple)
8 Videos
- PROBABILITY AND STATISTICSBOOK - CENGAGECHAPTER - PROBABILITY AND STATISTICSEXERCISE - Question Bank
24 Videos
- PROBABILITY IIBOOK - CENGAGECHAPTER - PROBABILITY IIEXERCISE - JEE Advanced Previous Year
25 Videos
Similar Questions
n whole numbers are randomly chosen and multiplied. Now, match the following lists.
List I List IIa. The probability that the last digit is 1, 3, 7, or 9 isp. 8n−4n10nb. The probability that the last digit is 2, 4, 6, 8 is q. 5n−4n10nc. The probability that the last digit is 5 isr. 4n10nd. The probability that the last digit is zero iss. 10n−8n−5n+4n10n
View SolutionIf the probability of a six digit number N whose six digit are 1,2,3,4,5,6 written as random order is divisible by 6 is p, then the value of 1/p is__________.
View SolutionIf A and B are any two events, then the probability that exactly one of them occur is
View SolutionIf two events A and B are such that P(Al)=0.3, P(B)=0.4 and P(A∩Bl)=0.5, then P(BA∪Bl) equals
View SolutionA signal which can be green or red with probability 45and15 respectively, is received by station A and then and 3 transmitted to station B. The probability of each station receiving the signal correctly is 34 If the signal received at station B is green, then the probability that the original signal was green is (a) 35 (b) 67 (c) 2023 (d) 920
View SolutionAn ellipse is inscribed in a circle and a point within the circle is chosen at random. If the probability that this point lies outside the ellipse is 23 then the eccentricity of the ellipse is: (A) 2√23 (B) √53 (C) 89 (D) 23
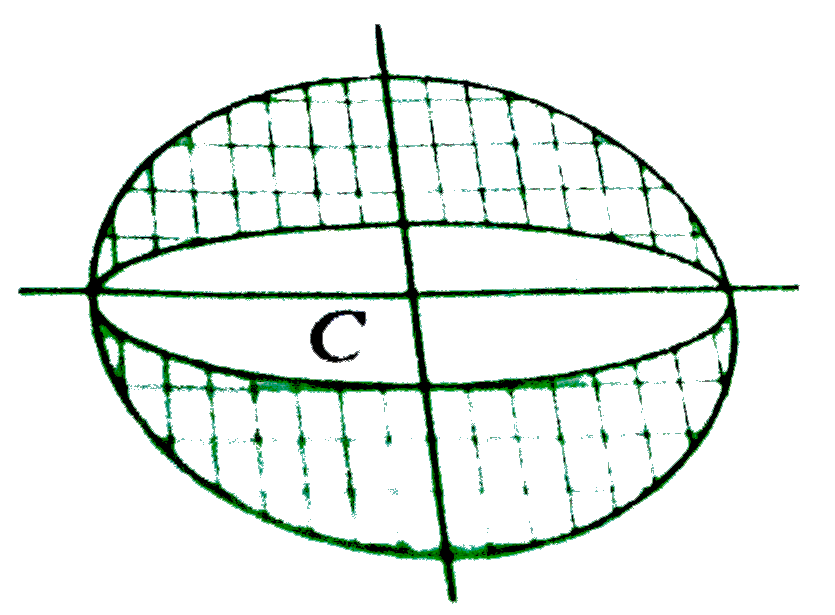
View SolutionThere are some experiment in which the outcomes cannot be identified discretely. For example, an ellipse of eccentricity 2√2/3 is inscribed in a circle and a point within the circle is chosen at random. Now, we want to find the probability that this point lies outside the ellipse. Then, the point must lie in the shaded region shown in Figure. Let the radius of the circle be a and length of minor axis of the ellipse be 2b. Given that
1−b2a2=89orb2a2=19
Then, the area of circle serves as sample space and area of the shaded region represents the area for favorable cases. Then, required probability is
p=Area of shaded regionArea of circle
=πa2−πabπa2=1−ba=1−13=23
Now, answer the following questions.

A point is selected at random inside a circle. The probability that the point is closer to the center of the circle than to its circumference is
View SolutionThere are some experiment in which the outcomes cannot be identified discretely. For example, an ellipse of eccentricity 2√2/3 is inscribed in a circle and a point within the circle is chosen at random. Now, we want to find the probability that this point lies outside the ellipse. Then, the point must lie in the shaded region shown in Figure. Let the radius of the circle be a and length of minor axis of the ellipse be 2b. Given that
1−b2a2=89orb2a2=19
Then, the area of circle serves as sample space and area of the shaded region represents the area for favorable cases. Then, required probability is
p=Area of shaded regionArea of circle
=πa2−πabπa2=1−ba=1−13=23
Now, answer the following questions.
Two persons A and B agree to meet at a place between 5 and 6 pm. The first one to arrive waits for 20 min and then leave. If the time of their arrival be independant and at random, then the probability that A and B meet is
View SolutionAn ellipse of eccentricity 2√23 is inscribed in a circle . A point is chosen inside the cirlce at random. The probaboility that the point lies outside the ellipse is
View SolutionA circle of maximum area is inscribed in an ellipse. If p is the probability that a point within the ellipse chosen at random lies outside the circle, then the eccentricity of the ellipse is
View SolutionAn ellipse of eccentricity 2√23 is inscribed in a circle and a point within the circle is chosen at random. Let the probability that this point lies outside the ellipse be p. Then the value of 105 p is
View SolutionAn ellipse is inscribed in its auxiliary circle and a point within the circle is chosen at random. If p is the probability that this point lies outside the ellipse and inside the auxiliary circle. Then 8p is equal to (where eccentricity of the ellipse is √32)
(A) 3 (B) 4 (C) 6 (D) 1
View SolutionAn ellipse is inscribed in its auxiliary circle and a point within the circle is chosen at random. If p is the probability that this point lies outside the ellipse and inside the auxiliary circle. Then 8p is equal to (where eccentricity of the ellipse is √32)
(A) 3 (B) 4 (C) 6 (D) 1
View SolutionAn eppipse of eccentricity 2√23 is inscribed in a circle and a point within the circle is chosen at random. The probability that this point lies outside the ellipse is
View SolutionAn ellipse of eccentricity 2√23 is inscribed in a circle and a point within the circle is chosen at random. The probability that this point lies outside the ellipse is
View SolutionEccentricity (2sqrt(3))/3 A point is randomly selected under an ellipse of a circle. The point is that the probability that the ellipse will be located outside is
View Solution
