If two distinct numbers m and n are chosen at random form the set {1, 2, 3, …, 100}, then find the probability that 2m+2n+1 is divisible by 3. Solution in Tamil
The correct Answer is:49198
2m+2n+1=(3−1)m+(3−1)n+1
=3k+(−1)m+(−1)n+1
This is divisible by 3 if both m and n are even.
∴ Required probabaility = .50C2.100C2=50×49100×99=49198
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - PROBABILITY I EXERCISE - Exercise 9.37videos
PROBABILITY I
- BOOK - CENGAGECHAPTER - PROBABILITY I EXERCISE - Exercise (Single)46videos
PROBABILITY I
- BOOK - CENGAGECHAPTER - PROBABILITY I EXERCISE - Exercise 9.16videos
PROBABILITY I
- BOOK - CENGAGECHAPTER - PROBABILITY AND STATISTICSEXERCISE - Question Bank24videos
PROBABILITY AND STATISTICS
- BOOK - CENGAGECHAPTER - PROBABILITY IIEXERCISE - JEE Advanced Previous Year25videos
PROBABILITY II
Similar Questions
AandB are two candidates seeking admission in ITT. The probability that A is selected is 0.5 and the probability that AandB are selected is at most 0.3. Is it possible that the probability of B getting selected is 0.9?
05:48View SolutionA sample space consists of 3 sample points with associated probabilities given as 2p,p2,4p−1. Then the value of p is
04:56View SolutionWhich of the following cannot be valid assignment of probabilities for outcomes of sample space S={W1,W2,W3,W4,W5,W6,W7}
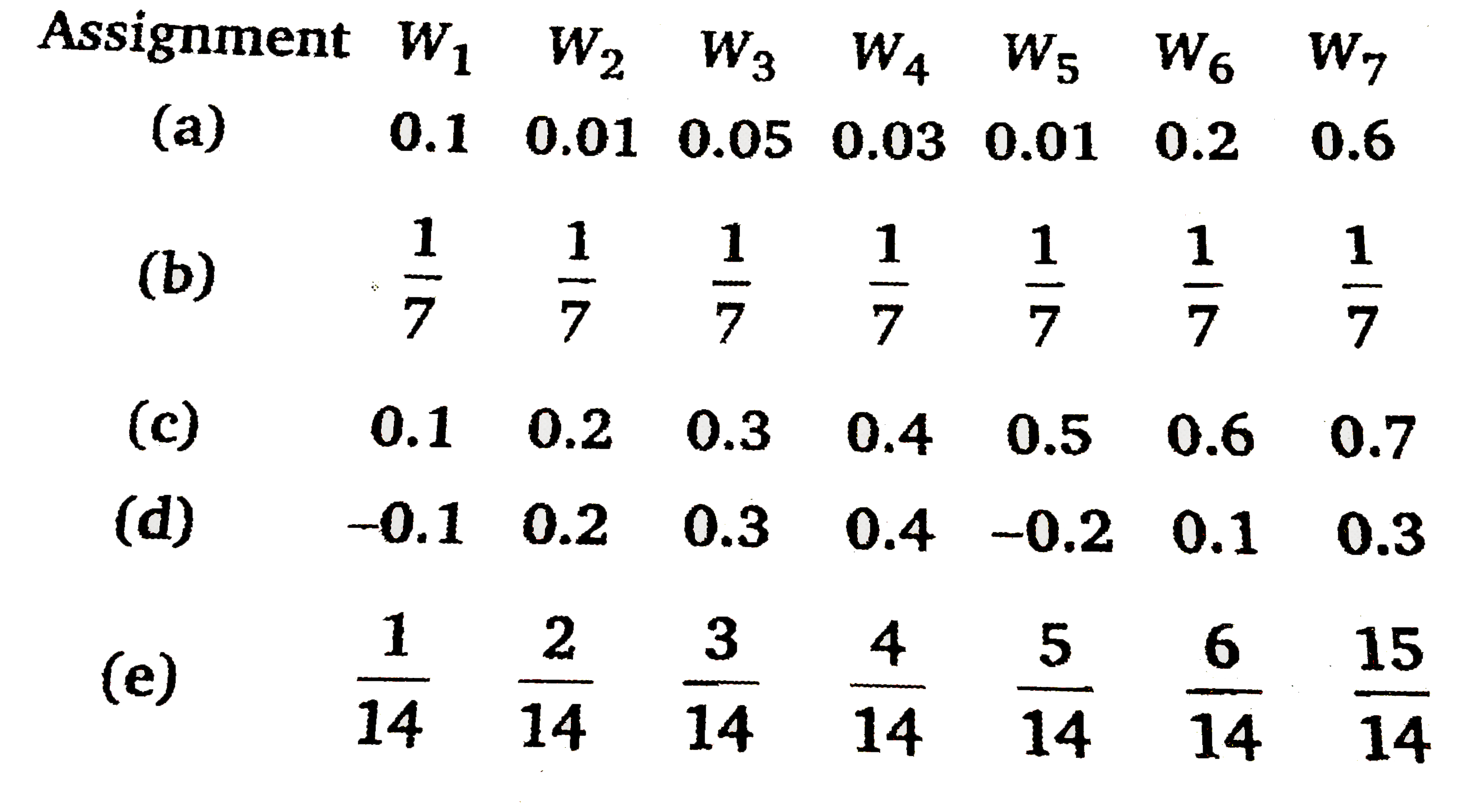 View Solution
View SolutionIf two events A and B are such that P(Al)=0.3, P(B)=0.4 and P(A∩Bl)=0.5, then P(BA∪Bl) equals
07:33View SolutionA signal which can be green or red with probability 45and15 respectively, is received by station A and then and 3 transmitted to station B. The probability of each station receiving the signal correctly is 34 If the signal received at station B is green, then the probability that the original signal was green is (a) 35 (b) 67 (c) 2023 (d) 920
01:21View SolutionIf two distinct numbers m and n are chosen at random form the set {1, 2, 3, …, 100}, then find the probability that 2m+2n+1 is divisible by 3.
02:21View Solution3 distinct integers are selected at random form 1, 2, 3, …, 20. find out the probability that the sum is divisible by 5
01:21View SolutionLet n=10λ+r,whereλ,r∈N,0≤r≤9. A number a is chosen at random from the set {1, 2, 3,…, n} and let pn denote the probability that (a2−1) is divisible by 10.
If 1≤r≤8, then np_n equals03:34View SolutionIf the integers m and n are chosen at random between 1 and 100, then the probability that a number of the form 7m+7n is divisible by 5, equals :
06:17View SolutionIf the integers m and n are chosen at random between 1 and 100, then atmost distinct numbers of the form 7m+7n is divisible by 5 equals to :
03:36View SolutionIf two distinct numbers m and n are chosen at random form the set {1, 2, 3, …, 100}, then find the probability that 2m+2n+1 is divisible by 3.
07:59View SolutionIf the integers m and n are chosen at random between 1 and 100, then atmost distinct numbers of the form 7m+7n is divisible by 5 equals to :
06:18View Solution3 distinct integers are selected at random form 1, 2, 3, …, 20. find out the probability that the sum is divisible by 5
05:18View Solution3 distinct integers are selected at random form 1, 2, 3, …, 20. find out the probability that the sum is divisible by 5
06:25View SolutionLet n=10λ+r,whereλ,r∈N,0≤r≤9. A number a is chosen at random from the set {1, 2, 3,…, n} and let pn denote the probability that (a2−1) is divisible by 10.
If 1≤r≤8, then np_n equalsView Solution
