Let the nine different letters A,B,C…I∈{1,2,3,…,9}. Then find the probability that product (A−1)(B−1)…(I−9) is an even number.Solution in Tamil
The correct Answer is:1
Given set of number is {1, 2, ……, 9} in which 4 are even and 5 are odd, so in the given product it is not possible to arrange to substract only even number from odd number, there must be at least one factor involving substraction of an odd number from another odd number. So at least one of the factor is even. Hence, product is always even.
∴ Required probability = 1
Topper's Solved these Questions
- PROBABILITY I BOOK - CENGAGECHAPTER - PROBABILITY I EXERCISE - Exercise 9.3
7 Videos
- PROBABILITY I BOOK - CENGAGECHAPTER - PROBABILITY I EXERCISE - Exercise (Single)
46 Videos
- PROBABILITY I BOOK - CENGAGECHAPTER - PROBABILITY I EXERCISE - Exercise 9.1
6 Videos
- PROBABILITY AND STATISTICSBOOK - CENGAGECHAPTER - PROBABILITY AND STATISTICSEXERCISE - Question Bank
24 Videos
- PROBABILITY IIBOOK - CENGAGECHAPTER - PROBABILITY IIEXERCISE - JEE Advanced Previous Year
25 Videos
Similar Questions
AandB are two candidates seeking admission in ITT. The probability that A is selected is 0.5 and the probability that AandB are selected is at most 0.3. Is it possible that the probability of B getting selected is 0.9?
View SolutionA sample space consists of 3 sample points with associated probabilities given as 2p,p2,4p−1. Then the value of p is
View SolutionWhich of the following cannot be valid assignment of probabilities for outcomes of sample space S={W1,W2,W3,W4,W5,W6,W7}
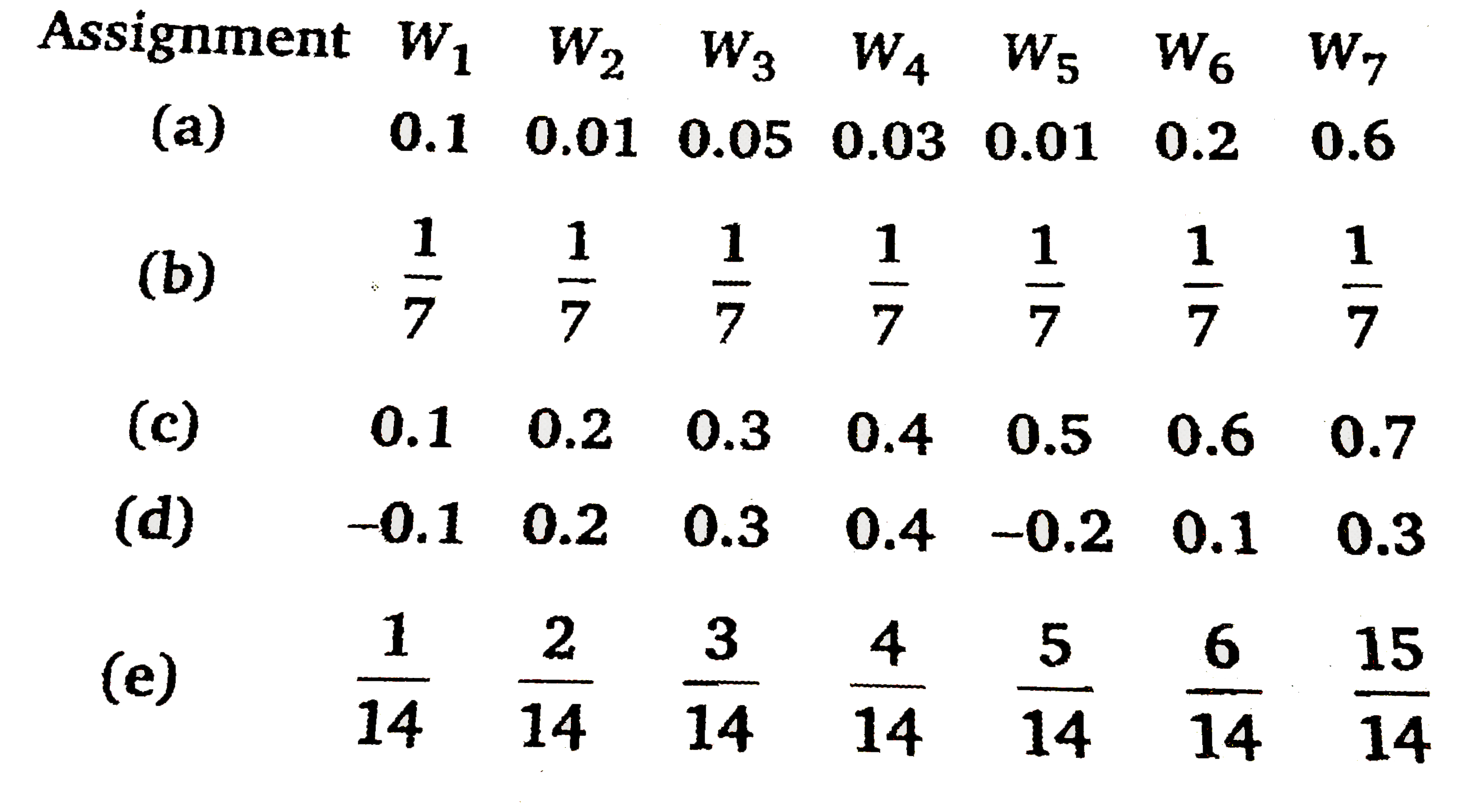
View SolutionIf two events A and B are such that P(Al)=0.3, P(B)=0.4 and P(A∩Bl)=0.5, then P(BA∪Bl) equals
View SolutionA signal which can be green or red with probability 45and15 respectively, is received by station A and then and 3 transmitted to station B. The probability of each station receiving the signal correctly is 34 If the signal received at station B is green, then the probability that the original signal was green is (a) 35 (b) 67 (c) 2023 (d) 920
View SolutionThe value of i5+i6+i7+i8+i91+i is (a) 12(1+i) (b) 12(1−i) (c) 1 (d) 12
View SolutionWhen simplified (−127)−23 is 9 (b) −9 (c) 19 (d) −19
View SolutionIn Q. No. 115, the probability that the digit is even, is 49 (b) 59 (c) 19 (d) 23
View SolutionFind the mean and standard deviation of the following probability distribution: xi:0 1 2 3 4 5 pi:16 518 29 16 19 118
View SolutionIf a+b+c=1,a^(2)+b^(2)+c^(2)=9 and a^(3)+b^(3)+c^(3)=1, then (1)/(a)+(1)/(b)+(1)/(c) is (i)0 (ii) -1(iii)1(iv)3
View SolutionThe average of the first nine prime numbers is (a) 9 (b) 11 (c) 1119 (d) 1129
View Solutionfind(a+b)-:(a-b) if (i)a=(1)/(3),b=(3)/(5)(i)a=-(1)/(13),b=(4)/(9)(iii)a=-(6)/(7)
View SolutionLet the nine different letters A,B,C…I∈{1,2,3,…,9}. Then find the probability that product (A−1)(B−1)…(I−9) is an even number.
View Solutionज्ञात कीजिए :
(a)(i)234 का 12 (ii)429 का 12 (b)(i)356 का 58 (ii)923 का 58
View SolutionFind the value of b2−4ac, if
(i) a=3,b=9,c=6 (ii) a=2,b=−8,c=8
(iii) a=1,b=1,c=1.
View Solutionवक्तव I यदि a,b,c एक सम प्राकृतिक संख्या है तब △=∣∣ ∣∣a−1aa+1b−1bb+1c−1cc+1∣∣ ∣∣ एक सम प्राकृतिक संख्या होगी
वक्तव II दो सम प्राकृतिक संख्या का योगफल तथा गुणनफल भी सदैव एक सम प्राकृतिक संख्या होगी
View Solution
