The vertices of a triangle lie on the lines , respectively, and the side passes through the point . If is a rhombus lying in the first quadrant, being the origin, find the equation of the line Solution in Tamil
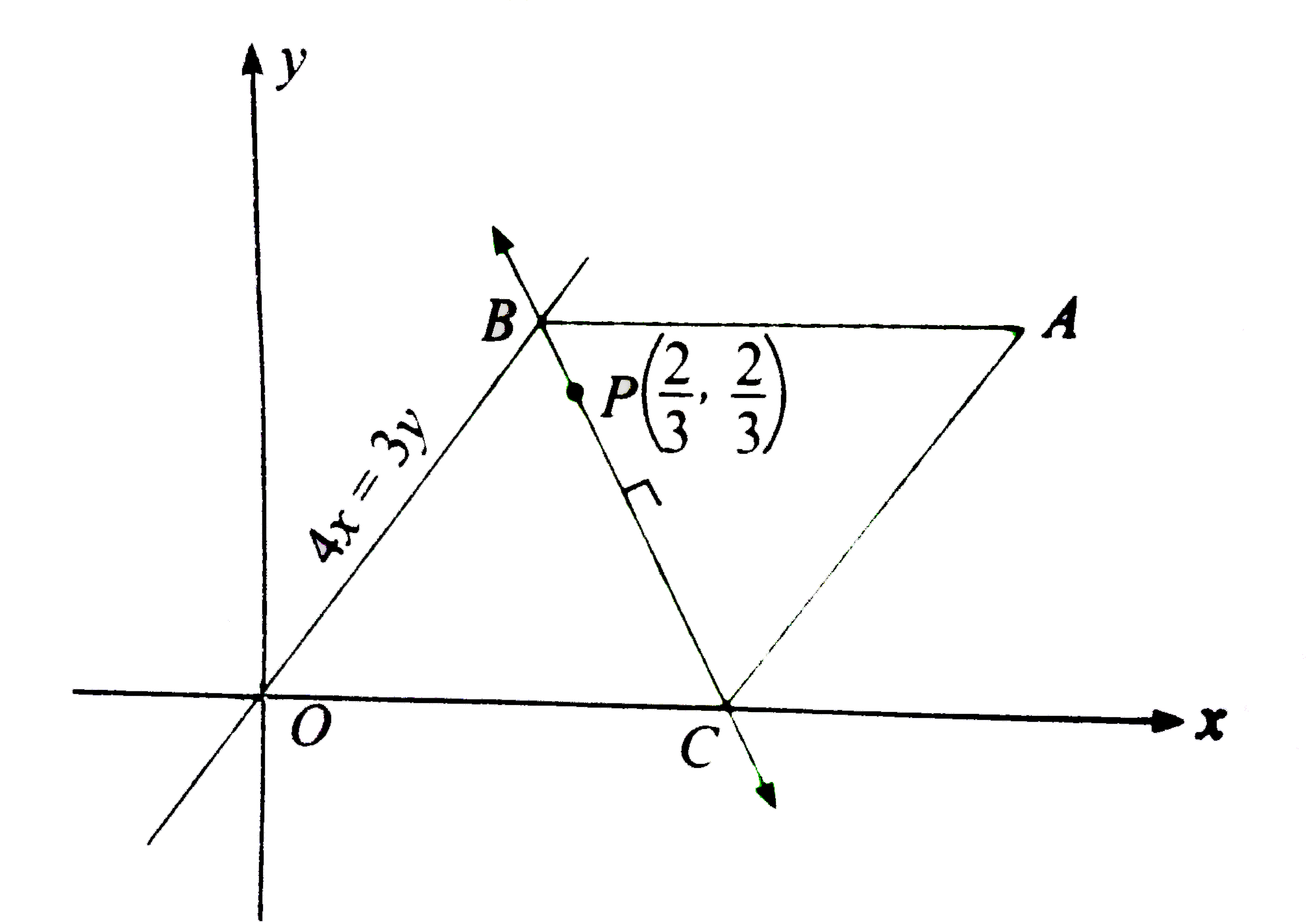
Diagonals of rhombus are equally inclined to the sides.
So, diagonals are parallel to or coincident with the angle bisectors of sides.
Equations of bisectors of sides OC and OB of rhombus are
or x-2y=0 and 2x+y=0
Clearly, diagonal BC is parallel to the bisector 2x+y=0.
So, equation BC is
or 2x+y-2=0
Similar Questions
The vertices BandC of a triangle ABC lie on the lines 3y=4xandy=0 , respectively, and the side BC passes through the point (23,23) . If ABOC is a rhombus lying in the first quadrant, O being the origin, find the equation of the line BC.
View SolutionThe sides ABandAC of a triangle ABC are respectively 2x+3y=29andx+2y=16 respectively. If the mid-point of BCis(5,6) then find the equation of BC.
View SolutionThe equations of the perpendicular bisectors of the sides ABandAC of triangle ABC are x−y+5=0 and x+2y=0 , respectively. If the point A is (1,−2) , then find the equation of the line BC.
View SolutionThe equations of the perpendicular bisectors of the sides A Ba n dA C of triangle A B C are x-y+5=0 and x+2y=0 , respectively. If the point A is (1,-2) , then find the equation of the line B Cdot
View SolutionIn a triangle ABC , the bisectors of angles BandC lies along the lines x=yandy=0. If A is (1,2) , then the equation of line BC is (a) 2x+y=1 (b) 3x−y=5 (c) x−2y=3 (d) x+3y=1
View SolutionThe base of the pyramid A O B C is an equilateral triangle O B C with each side equal to 4sqrt(2),O is the origin of reference, A O is perpendicualar to the plane of O B C and | vec A O|=2. Then find the cosine of the angle between the skew straight lines, one passing though A and the midpoint of O Ba n d the other passing through O and the mid point of B Cdot
View SolutionThe equations of the perpendicular bisectors of the sides ABandAC of triangle ABC are x−y+5=0 and x+2y=0 , respectively. If the point A is (1,−2) , then find the equation of the line BC.
View Solution