Three liquids of densities ρ1,ρ2 and ρ3 (with ρ1>ρ2>ρ3), having the same value of surface tension T, rise to the same height in three identical capillaries. The angles of contact θ1,θ2 and θ3 obey
π2<θ1<θ2<θ3<π
π>θ1>θ2>θ3>π2
π2>θ1>θ2>θ3≥0
0≤θ1<θ2<θ3<π2
The correct Answer is:D
h=2Tcosθρgr
As r, h, T are same,cosθρ= constant
⇒cosθ1ρ1=cosθ2ρ2=cosθ3ρ3
As ρ1>ρ2>ρ3
⇒cosθ1>cosθ2>cosθ3⇒θ1<θ2<θ3
As water rises so θ must be acute
So, 0≤θ1<θ2<θ3<π/2
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF MATTERBOOK - PHYSICS WALLAHCHAPTER - MECHANICAL PROPERTIES OF MATTEREXERCISE - Level -II
30 Videos
- MECHANICAL PROPERTIES OF MATTERBOOK - PHYSICS WALLAHCHAPTER - MECHANICAL PROPERTIES OF MATTEREXERCISE - NEET Past 5 Yeats Questions
16 Videos
- MAGNETISM AND MATTER BOOK - PHYSICS WALLAHCHAPTER - MAGNETISM AND MATTER EXERCISE - NEET PAST 5 YEARS QUESTIONS
10 Videos
- MOTION IN A PLANE BOOK - PHYSICS WALLAHCHAPTER - MOTION IN A PLANE EXERCISE - NEET Past 5 years Questions
10 Videos
Similar Questions
A rectangular tube of uniform cross section has three liquids of densities ρ1,ρ2 and ρ3. Each liquid column has length l equal to length of sides of the equilateral triangle. Find the length x of the liquid of density ρ1 in the horizontal limb of the tube, if the triangular tube is kept in the vertical plane.

View Solution(i) One end of a uniform glass capillary tube of radius r=0.025 cm is immersed vertically in water to a depth h=1cm. Contact angle is 0∘, surface tension of water is 7.5×10–2N/m, density of water is ρ=103kg/m3 and atmospheric pressure is Po=105N/m2
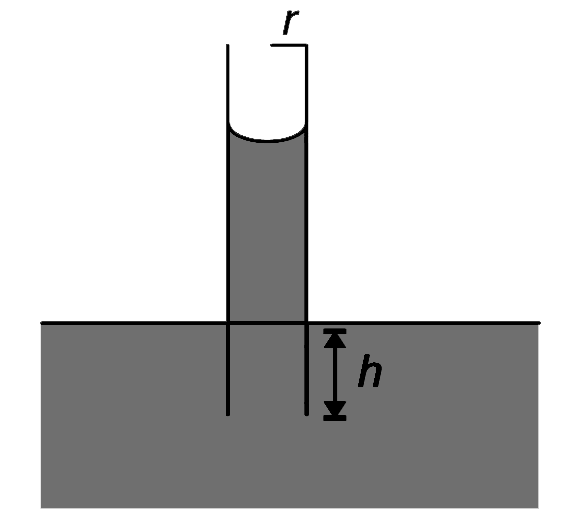
Find the excess pressure to be applied on the water in the capillary tube so that -
(a) The water level in the tube becomes same as that in the vessel.
(b) Is it possible to blow out an air bubble out of the tube by increasing the pressure? (ii) A container contains two immiscible liquids of density ρ1 and ρ2(ρ2>ρ1). A capillary of radius r is inserted in the liquid so that its bottom reaches up to denser liquid and lighter liquid does not enter into the capillary. Denser liquid rises in capillary and attain height equal to h which is also equal to column length of lighter liquid. Assuming zero contact angle find surface tension of the heavier liquid.
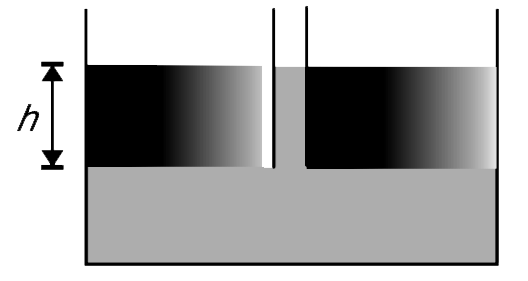
View Solution
Knowledge Check
Three liquids of densities ρ1,ρ2 and ρ3 (with ρ1>ρ2>ρ3), having the same value of surface tension T, rise to the same height in three identical capillaries. The angles of contact θ1,θ2 and θ3 obey
Aπ2<θ1<θ2<θ3<πBπ>θ1>θ2>θ3>π2Cπ2>θ1>θ2>θ3≥0D0≤θ1<θ2<θ3<π2Three liquids of densities ρ1,ρ2 and ρ3 (with ρ1>ρ2>ρ3), having the same value of surface tension T, rise to the same height in three identical capillaries. The angles of contact θ1,θ2 and θ3 obey
Aπ2<θ1<θ2<θ3<πBπ>θ1>θ2>θ3>π2Cπ2>θ1>θ2>θ3≥0D0≤θ1<θ2<θ3<π2Three liquids of densities ρ1,ρ2 and ρ3 (with ρ1>ρ2>ρ2) having the same value of surface tension T, rise to the same height in three identical capillaries. The angles of contact θ1,θ2 and θ3 obey
Aπ2<θ1<θ2<θ<πBπ>θ1>θ2>θ3>π2Cπ2>θ1>θ2>θ3≥0D0≤θ1<θ2<θ3<π2
Three liquids having densities ρ1,ρ2,ρ3 are filled in a U-tube. Length of each liquid column is equal to I, ρ1>ρ2>ρ3 and liquids remain at rest (relative to the tube) in the position shown in the figure. It is possible that

View SolutionTwo wires of equal diameters, of resistivities ρ1 and ρ2 and length l1 and l2, respectively of the combination is
View SolutionA solid sphere of radius r is floating at the interface of two immiscible liquids of densities ρ1 and ρ2(ρ2>ρ1), half of its volume lying in each. The height of the upper liquid column from the interface of the two liquids is h. The force exerted on the sphere by the upper liquid is (atmospheric pressure =p0 and acceleration due to gravity is g):
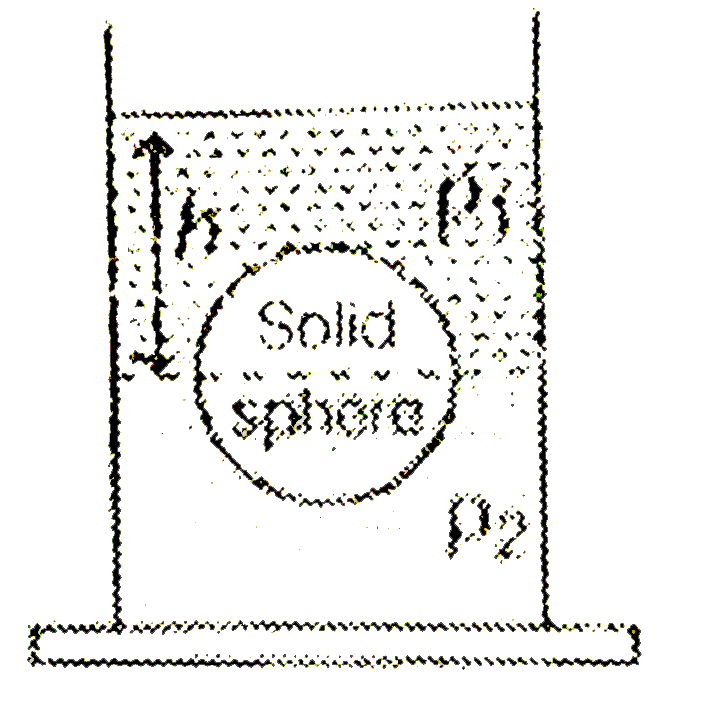
View SolutionTwo liquids of densities 2ρ and ρ having their volumes in the ratio 3:2 are mixed together. Density of the mixture will be
View SolutionThree identical vessels are filled to the same height with three different liquids A, B and C(ρA>ρB>ρC). The pressure at the base will be
View Solution
