Two particles of equal masses m go round a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is v=√GmnR. Find the value of n.
v=12R√1GM
v=√Gm2R
v=12√GmR
v=√4GmR
The correct Answer is:C
Centripetal force provided by the gravitational force of attraction between two particles
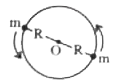
i.e. mv2R=GM×m(2R)2
v=12√GmR
Topper's Solved these Questions
- BOOK - PHYSICS WALLAHCHAPTER - GRAVITATIONEXERCISE - NEET Past 5 Years Questions13videos
GRAVITATION
- BOOK - PHYSICS WALLAHCHAPTER - GRAVITATIONEXERCISE - NEET Past 5 Years Questions13videos
GRAVITATION
- BOOK - PHYSICS WALLAHCHAPTER - GENERAL PRINCIPLES AND PROCESSES OF ISOLATION OF ELEMENTSEXERCISE - NEET Past 5 Years Questions14videos
GENERAL PRINCIPLES AND PROCESSES OF ISOLATION OF ELEMENTS
- BOOK - PHYSICS WALLAHCHAPTER - KINETIC THEORY EXERCISE - NEET PAST 5 YEARS QUESTIONS11videos
KINETIC THEORY
Similar Questions
Two particles of equal mass go round a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
View SolutionTwo particles of equal mass (m) move in a circle of radius (r ) under the action of their mutual gravitational attraction. Find the speed of each particle.
View Solution
Knowledge Check
- Question 1 - Select One
Two particles of equal mass go around a circle of radius R under the action of their mutual gravitational attraction. The speed v of earth particle is
A13√GmRB12√GmRC12√RGmD√GmR - Question 2 - Select One
Two particles of same mass m go around a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is ,
AV=12R√1GmBV=√GM2RCV=12√GmRDV=√4GmR - Question 3 - Select One
Two particles of equal mass m go around a circle of radius R under the action the of their mutual gravitational attraction . The speed v of each particle is
A12√GmRB√4GMRC12R√1GmD√Gm2R
For particles of equal massses M move along a circle of radius R under th action of their mutual gravitational attraction. Find the speed of each particle.
View Solution_S01_003_Q01.png)
Two particles of equal mass (m) each move in a circle of radius (r) under the action of their mutual gravitational attraction find the speed of each particle.View SolutionTwo particles each of equal mass (m) move along a circle of radius (r) under the action of their mutual dravitational. Find the speed of each particle.
 View Solution
View SolutionFour particles each of mass M move along a circle of radius R under the action of their mutula gravitational attraction the speed of each paritcles is
View SolutionFour particles each of mass M move along a circle of radius R under the action of their mutula gravitational attraction the speed of each paritcles is
View Solution
