A body of mass m = 10 kg is attached to a wire of length 0.3m. The maximum angular velocity with which it can be rotated in a horizontal circle is (Given, breaking stress of wire =4.8×107Nm−2 and area of cross-section of a wire =10−6m2)
The correct Answer is:4
Step by step video & image solution for A body of mass m = 10 kg is attached to a wire of length 0.3m. The maximum angular velocity with which it can be rotated in a horizontal circle is (Given, breaking stress of wire = 4.8 xx 10^(7) Nm^(-2) and area of cross-section of a wire = 10^(-6) m^(2)) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
A bob of mass 10 kg is attached to wire 0.3 m long. Its breaking stress is 4.8×107N/m2. The area of cross section of the wire is 10−6m2. The maximum angular velocity with which it can be rotated in a horizontal circle
View SolutionA bob of mass 10 kg is attached to wire 0.3 m long. Its breaking stress is 4.8×107N/m2. The area of cross section of the wire is 10−6m2. The maximum angular velocity with which it can be rotated in a horizontal circle
View SolutionA bob of mass 10kg is attached to a wire 0.3m long. Its breaking stress is 4.8×107N/m2. Then area of cross-section of the wire is 10−6m2. What is the maximum angular velocity with which it can be rotated in a horizontal circle?
View SolutionA mass of 20kg is attached to one end of a steel wire 50cm long and is rotated in a horizontal circle. The area of cross-section of the wrie is 10−6m2 and the breaking stress for it is 4.8×107Pa. Calculate the maximum velocity with which the mass can be rotated.
View SolutionFind the greatest length of copper wire, that can hang without breaking. Breaking stress =7.2×107N/m2. Density of copper 7.2g/cc.g=10m/s2.
View SolutionA copper wire of negligible mass, 1m length and cross-sectional area 10−6m2 is kept on a smooth horizontal table with one end fixed. A ball of mass 1kg is attached to the other end. The wire and the ball are rotating with an angular velocity of 20rad/s. If the elongation in the wire is 10−3m.
a. Find the Young's modulus of the wire (in terms of ×1011N/m2).
b. If for the same wire as stated above, the angular velocity is increased to 100rad/s and the wire breaks down, find the breaking stress (in terms of ×1010N/m2).View SolutionTwo blocks of masses 2 kg and 3kg are connected by a metal wire going over a smoother pulley as shown in figure. The breaking stress of the steel is 2×109Nm−2. What would be the minimum radius of the wire used if it not to break ? Take ,g=10ms−2
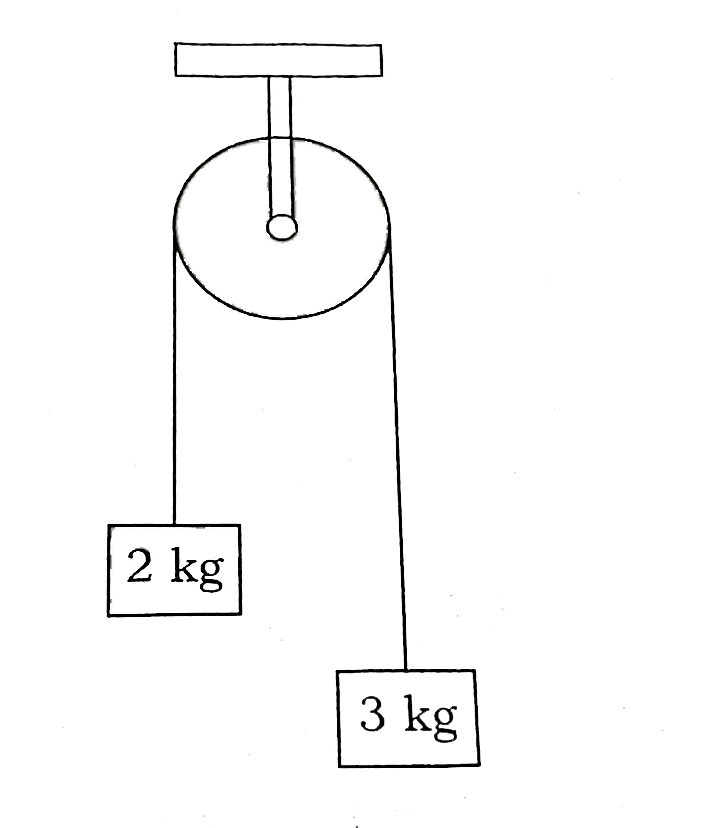 View Solution
View SolutionBreaking stress for a material is 2×108N/m2. What maximum length of the wire of this material can be taken t the wire does not break by own weight? Density of material = 5×103kg/m3
View SolutionFind the greatest length of steel wire that can hang vertically without breaking. Breaking stress of steel =8.0×108N/m2. Density of steel =8.0×103kg/m3. Take g=10m/s2.
View SolutionA body of mass 3.14kg is suspended from one end of a wire of length 10m. The radius of cross-section of the wire is changing uniformly from 5×10−4m at the top (i.e. point of suspension) to 9.8×10−4m at the bottom . Young's modulus of elasticity is 2×1011N/m2. The change in length of the wire is
View Solution


