Two particles of masses m and 3m approach each other with different velocities. After collision, the particle of mass m has velocity →v in their centre of mass frame. Velocity of particle of mass 3m in the centre of mass frame is
(a)−2→v
(b)−→v2
(c)−→v3
(d)→v4
The correct Answer is:C
To solve the problem, we need to find the velocity of the particle of mass 3m in the center of mass frame after the collision, given that the particle of mass m has a velocity →v in that frame.
Step 1: Understand the System
We have two particles:
- Particle 1 with mass m and velocity →v1 (approaching).
- Particle 2 with mass 3m and velocity →v2 (approaching).
After the collision, we know that the velocity of particle 1 (mass m) in the center of mass frame is →v.
Step 2: Center of Mass Frame
In the center of mass frame, the total momentum is zero. Therefore, we can write the equation for momentum conservation:
m→v1+3m→v2=0
This implies:
→v1+3→v2=0
or
→v1=−3→v2
Step 3: Relate Velocities in the Center of Mass Frame
After the collision, we need to express the velocity of the second particle (mass 3m) in terms of the known velocity →v of the first particle (mass m):
Let the velocity of the particle of mass 3m in the center of mass frame be →v′.
Using the conservation of momentum in the center of mass frame:
m→v+3m→v′=0
This leads to:
→v+3→v′=0
or
3→v′=−→v
Step 4: Solve for →v′
Now, we can solve for →v′:
→v′=−→v3
Conclusion
The velocity of the particle of mass 3m in the center of mass frame is:
→v′=−→v3
Final Answer
The velocity of the particle of mass 3m in the center of mass frame is −→v3.
We have two particles:
- Particle 1 with mass m and velocity →v1 (approaching).
- Particle 2 with mass 3m and velocity →v2 (approaching).
In the center of mass frame, the total momentum is zero. Therefore, we can write the equation for momentum conservation:
m→v1+3m→v2=0
This implies:
→v1+3→v2=0
or
→v1=−3→v2
After the collision, we need to express the velocity of the second particle (mass 3m) in terms of the known velocity →v of the first particle (mass m):
Let the velocity of the particle of mass 3m in the center of mass frame be →v′.
m→v+3m→v′=0
This leads to:
→v+3→v′=0
or
3→v′=−→v
Now, we can solve for →v′:
→v′=−→v3
The velocity of the particle of mass 3m in the center of mass frame is:
→v′=−→v3
The velocity of the particle of mass 3m in the center of mass frame is −→v3.
Similar Questions
Knowledge Check
The escape velocity of a particle of mass 'm'
Avaries as m2Bvaries as mCvaries as m−1Dis independent of mass
Two particles of a mass 2m and m are tied with an inextensible string the particle of mass m is given a speed V as shown in the figure. Find the speed with which the particle of mass 2m starts moving.
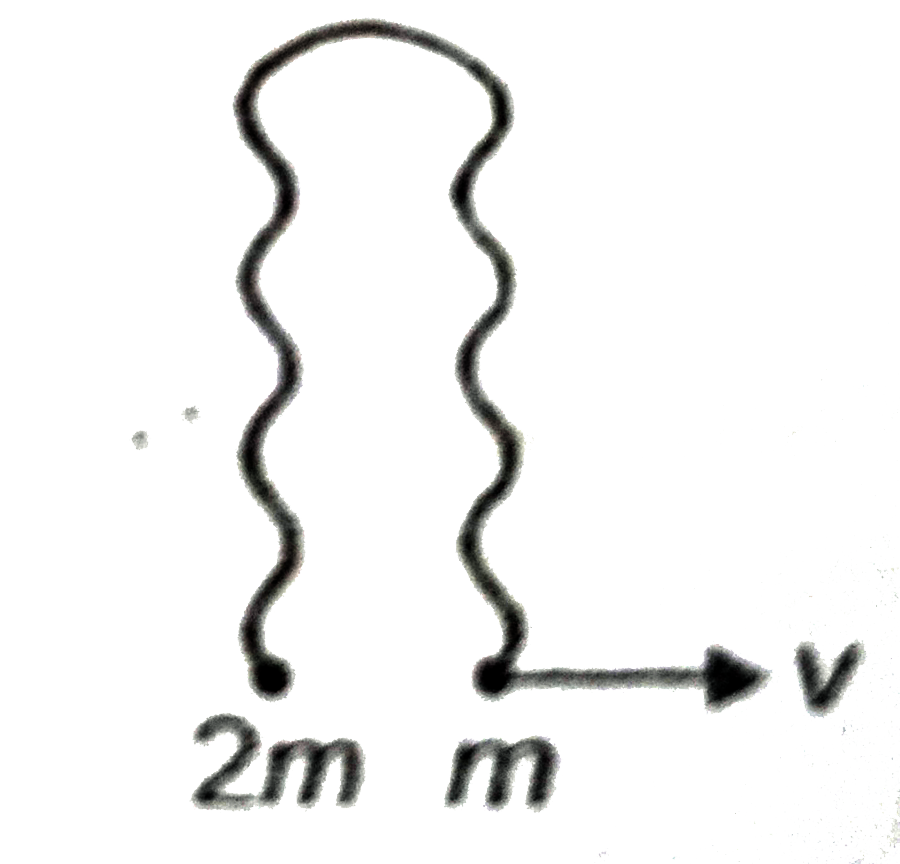
View SolutionTwo particles of a mass 2m and m are tied with an inextensible string the particle of mass m is given a speed V as shown in the figure. Find the speed with which the particle of mass 2m starts moving.

View SolutionA particle of mass 2m moving with velocity v strikes a stationary particle of mass 3m and sticks to it . The speed of the system will be
View SolutionA particle of mass m travelling with velocity v and kinetic energy E collides elastically to another particle of mass nm, at rest. What is the fraction of total energy retained by the particle of mass m?
View SolutionStatement-1: Two particles of mass 1 kg and 3 kg move towards each other under their mutual force of attraction. No other force acts on them. When the relative velocity of approach of the two particles is 2m/s, their centre of mass has a velocity of 0.5m/s. When the relative velocity of approach becomes 3m/s the velocity of the centre of mass is 0.75m/s.
Statement-2: The total kinetic energy as seen from ground is 12μv2rel+12mv2c and in absence of external force, total energy remains conserved.
View SolutionTwo particles of mass m1 and m2 are approaching towards each other under their mutual gravitational field. If the speed of the particle is v, the speed of the center of mass of the system is equal to :
View SolutionTwo particles of mass 1 kg and 3 kg move towards each other under their mutual force of attraction. No other force acts on them. When the relative velocity of approach of the two particles is 2m/s, their centre of mass has a velocity of 0.5 m/s. When the relative velocity of approach becomes 3m/s, the velocity of the centre of mass is 0.75 m/s.
View Solution

