Charge is distributed uniformly in some space. The net flux passing through the surface of an imaginary cube of side a in the space is ϕ. The net flux passing through the surface of an imaginary sphere of radius a in the space will be
ϕ
34πϕ
2π3ϕ
4π3ϕ
The correct Answer is:D
To solve the problem, we will use Gauss's Law, which states that the electric flux through a closed surface is proportional to the charge enclosed by that surface.
1. Understand the Problem: We have a uniform charge distribution in space. We know the electric flux through a cube of side a is given as φ. We need to find the electric flux through a sphere of radius a.
2. Calculate Charge Enclosed in the Cube:
- The volume of the cube, \( V_{\text{cube}} \), is given by:
\(
V_{\text{cube}} = a^3
\)
- Let the volume charge density be \( \rho \). The total charge \( Q_{\text{cube}} \) enclosed in the cube is:
\(
Q_{\text{cube}} = \rho \cdot V_{\text{cube}} = \rho \cdot a^3
\)
3. Apply Gauss's Law for the Cube:
- According to Gauss's Law:
\(
\Phi_{\text{cube}} = \frac{Q_{\text{cube}}}{\epsilon_0} = \frac{\rho \cdot a^3}{\epsilon_0}
\)
- We know from the problem statement that \( \Phi_{\text{cube}} = \phi \). Therefore:
\(
\phi = \frac{\rho \cdot a^3}{\epsilon_0}
\)
4. Calculate Charge Enclosed in the Sphere:
- The volume of the sphere, \( V_{\text{sphere}} \), is given by:
\(
V_{\text{sphere}} = \frac{4}{3} \pi a^3
\)
- The total charge \( Q_{\text{sphere}} \) enclosed in the sphere is:
\(
Q_{\text{sphere}} = \rho \cdot V_{\text{sphere}} = \rho \cdot \frac{4}{3} \pi a^3
\)
5. Apply Gauss's Law for the Sphere:
- According to Gauss's Law:
\(
\Phi_{\text{sphere}} = \frac{Q_{\text{sphere}}}{\epsilon_0} = \frac{\rho \cdot \frac{4}{3} \pi a^3}{\epsilon_0}
\)
6. Relate the Flux through the Sphere to the Flux through the Cube:
- We already know that \( \phi = \frac{\rho \cdot a^3}{\epsilon_0} \). Therefore, we can express \( \Phi_{\text{sphere}} \) in terms of \( \phi \):
\(
\Phi_{\text{sphere}} = \frac{4}{3} \pi \cdot \frac{\rho \cdot a^3}{\epsilon_0} = \frac{4}{3} \pi \cdot \phi
\)
7. Final Answer:
- Thus, the net flux passing through the surface of the imaginary sphere of radius a is:
\(
\Phi_{\text{sphere}} = \frac{4}{3} \pi \phi
\)
- The volume of the cube, \( V_{\text{cube}} \), is given by:
\(
V_{\text{cube}} = a^3
\)
- Let the volume charge density be \( \rho \). The total charge \( Q_{\text{cube}} \) enclosed in the cube is:
\(
Q_{\text{cube}} = \rho \cdot V_{\text{cube}} = \rho \cdot a^3
\)
- According to Gauss's Law:
\(
\Phi_{\text{cube}} = \frac{Q_{\text{cube}}}{\epsilon_0} = \frac{\rho \cdot a^3}{\epsilon_0}
\)
- We know from the problem statement that \( \Phi_{\text{cube}} = \phi \). Therefore:
\(
\phi = \frac{\rho \cdot a^3}{\epsilon_0}
\)
- The volume of the sphere, \( V_{\text{sphere}} \), is given by:
\(
V_{\text{sphere}} = \frac{4}{3} \pi a^3
\)
- The total charge \( Q_{\text{sphere}} \) enclosed in the sphere is:
\(
Q_{\text{sphere}} = \rho \cdot V_{\text{sphere}} = \rho \cdot \frac{4}{3} \pi a^3
\)
- According to Gauss's Law:
\(
\Phi_{\text{sphere}} = \frac{Q_{\text{sphere}}}{\epsilon_0} = \frac{\rho \cdot \frac{4}{3} \pi a^3}{\epsilon_0}
\)
- We already know that \( \phi = \frac{\rho \cdot a^3}{\epsilon_0} \). Therefore, we can express \( \Phi_{\text{sphere}} \) in terms of \( \phi \):
\(
\Phi_{\text{sphere}} = \frac{4}{3} \pi \cdot \frac{\rho \cdot a^3}{\epsilon_0} = \frac{4}{3} \pi \cdot \phi
\)
- Thus, the net flux passing through the surface of the imaginary sphere of radius a is:
\(
\Phi_{\text{sphere}} = \frac{4}{3} \pi \phi
\)
Similar Questions
Knowledge Check
The net magnetic flux through any closed surface, kept in a magnetic field is
AzeroBμ04πC4πμ0D4μ0π
When a 10 μC charge is enclosed by a closed surface, the flux passing through the surface is ϕ. Now another 10 µC charge is placed inside the closed surface, then the flux passing through the surface is ______.
View SolutionFlux passing through the shaded surface of a sphere when a point charge q is placed at the center is (radius of the sphere is R)
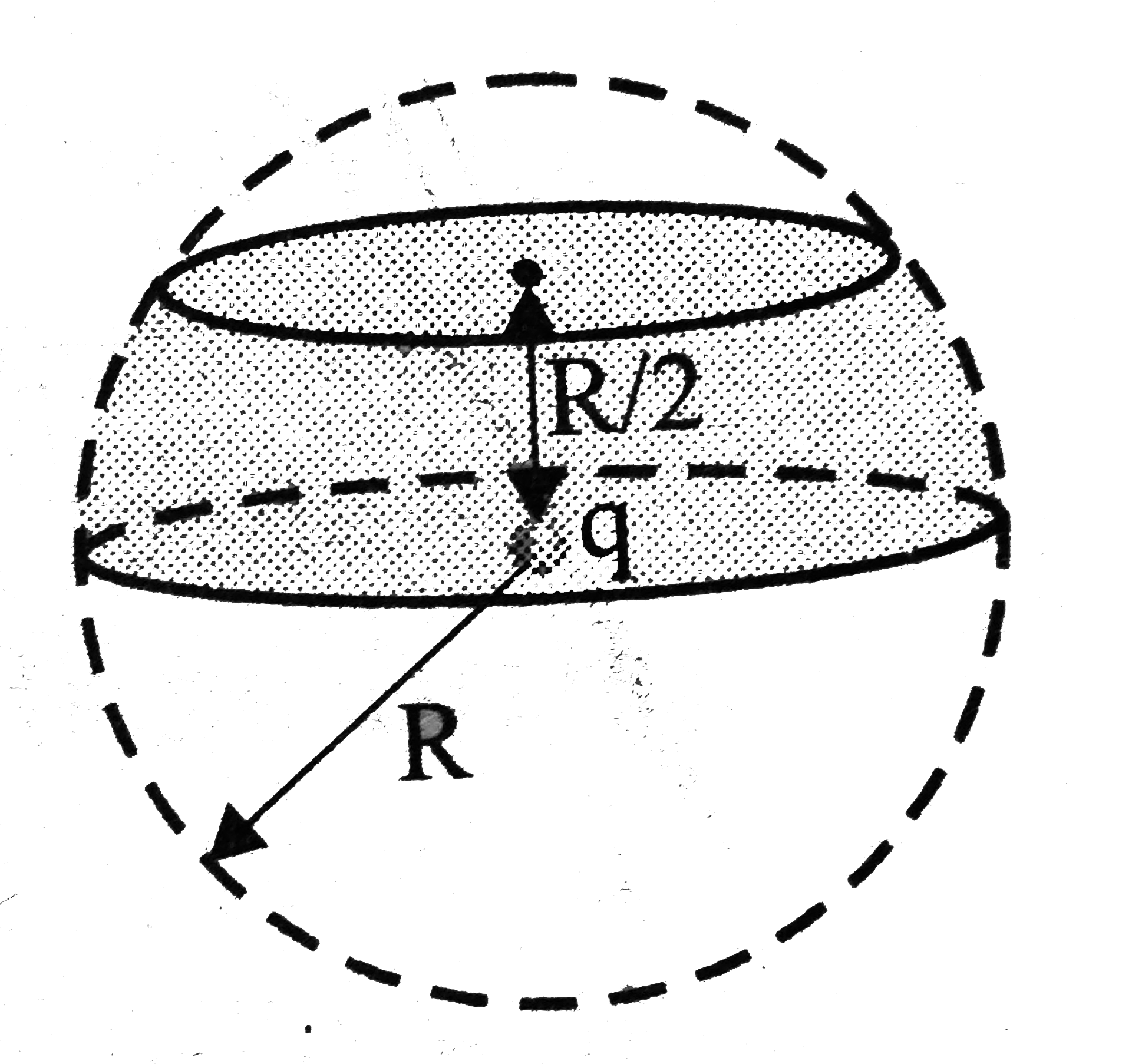
View SolutionA charge q is placed at the centre of a cube of side l what is the electric flux passing through two opposite faces of the cube ?
View SolutionA charge q is placed at the centre of a cube of side l what is the electric flux passing through two opposite faces of the cube ?
View SolutionA charge q is placed at the centre of a cube. What is the electric flux passing through the cube?
View SolutionThe net magnetic flux through any closed surface, kept in a magnetic field is
View SolutionA charge q0 is distributed uniformly on a ring of radius R. A sphere of equal radius R constructed with its centre on the circumference of the ring. Find the electric flux through the surface of the sphere.
View Solution

