Two capacitor and , charged with charges and then these are connected in series with an uncharged capacitor , as shown in figure. As the switch is closed :
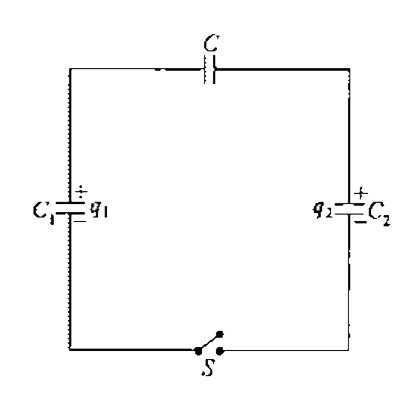
C gets charged in any condition
C gets charged only when
C gets charged only when
C gets charged when
The correct Answer is:D
Charge in the circuit flows only when potential difference across is either greater or less than that across
i.e.
Similar Questions
Two capacitors C1andC2 are connected with two batteries of emf ε1 and ε2. The circuit components are connected with a switch S as shown in. Initially the switch is open and the capacitors are charged. Find the heat produced when switch S is closed.
 .
.
View SolutionThere are two conductors of capacitance C and 2C are charged equally with charge +Q each and connected with a thin conducting wire and a switch as shown in figure. Find the final charges on the conductors after closing the switch.
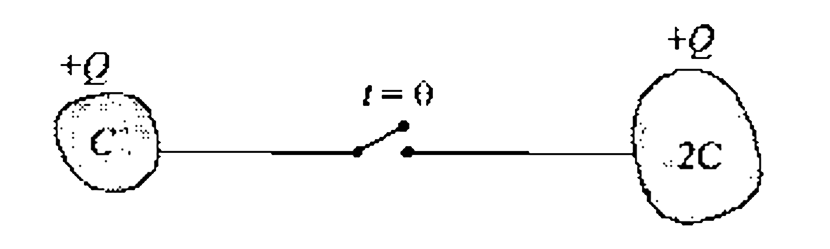
View Solution
Knowledge Check
Two capacitor each of capacitance C=1μF each charged to potential 100 V and 50 V respectively and connected across a uncharged capacitor 'C' = 1μF as shown in the figure if switch 'S' is closed then charge in the uncharged capacitor at equilibrium will be
 A503μCB50μCC25μCD1003μC
A503μCB50μCC25μCD1003μCThree capacitor C1=6F,C2=3F and C3=4F are separately charged with battery such that charge on each capacitor are 36C,24C and 40C respectively and then disconnected with the battery. After that they are connected in a circuit along with an uncharged capacitor C4=4F and a battery of emf =4 volts as shown figure. Now the switch S is closed. Choose is correct option (s).
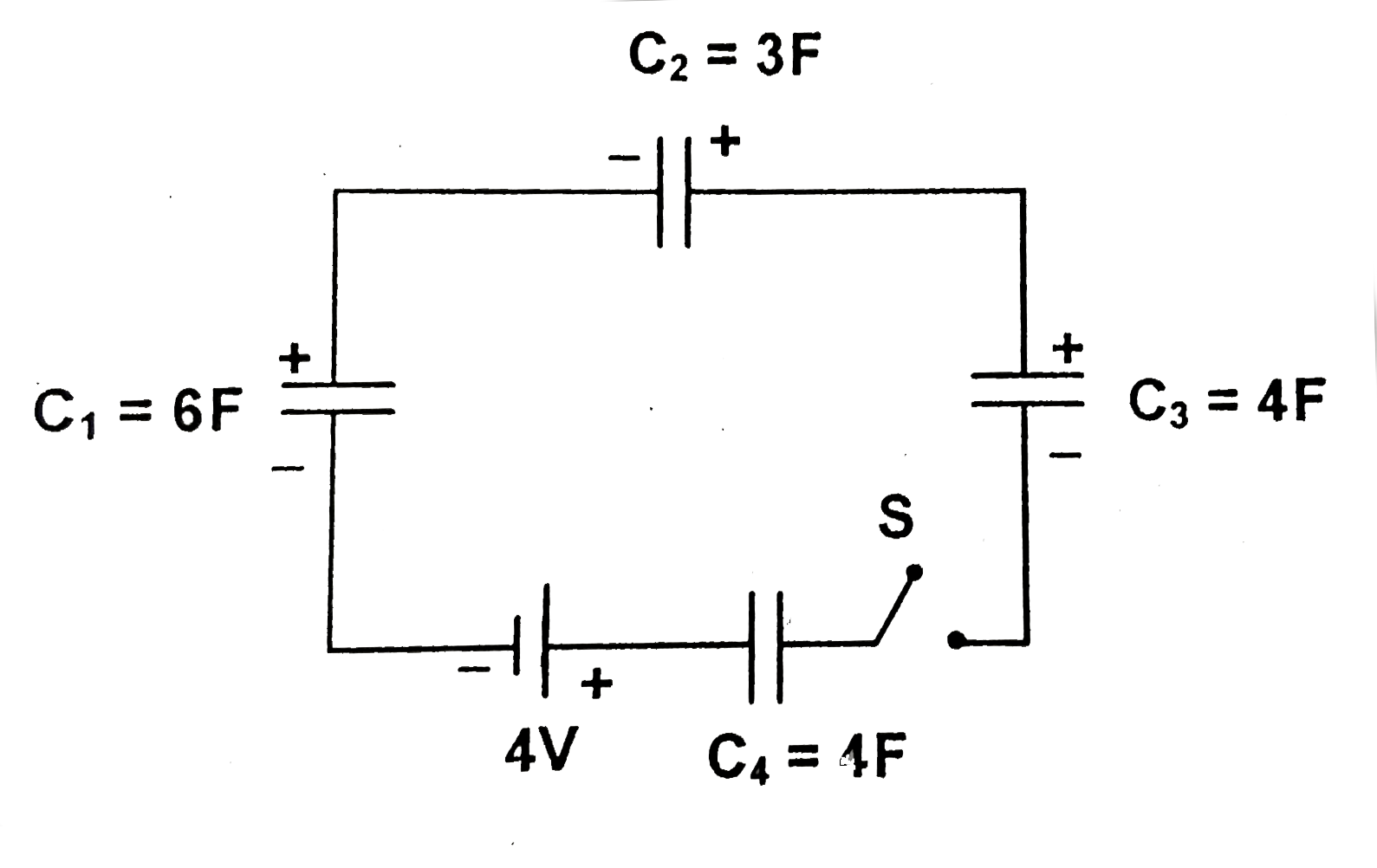 AFinal charge on capacitor C4=4CBFinal charge on capacitor C2=24CCFinal charge on capacitor C3=36CDAmount of charge flow in circuit = zero
AFinal charge on capacitor C4=4CBFinal charge on capacitor C2=24CCFinal charge on capacitor C3=36CDAmount of charge flow in circuit = zeroA capacitor of capacitance C1 is charged to a potential difference V and then connected with an uncharged capacitor of capacitance C2 a resistance R. The switch is closed at t = 0. Choose the correct option(s):
AThe initial current through the resistance is VRBThe current through the resistance as a function of time is i(t)=VRe−tτ where τ=R(C1C2C1+C2)CThe charge on capacitor C1 as a function of time is q1(t)=(C1VC1+C2)(C1+C2e−tτ)DAfter a long time, the potential difference across the capacitor C1is(C1C1+C2)V
Two capacitors A and B are connected in series with a battery as shown in the figure. When the switch S is closed and the two capacitors get charged fully, then

View SolutionA capacitor C1 is charged to a p.d.V. The charging battery is then removed and the capacitor is connected to an uncharged capacitor C2. The final p.d. across the combination is
View SolutionAfter the capacitor gets fully charged, S1 is opened and S2 is closed so that the inductor is connected in series with the capacitor. Then,
View SolutionTwo capacitorsC1andC2=2C1 are connected in a circuit with a switch between them as showu in the figure- 3.302. Initially the switch is open and C1 holds charge Q. The switch is closed. In steady state, the charge on the two capacitors will be given as :
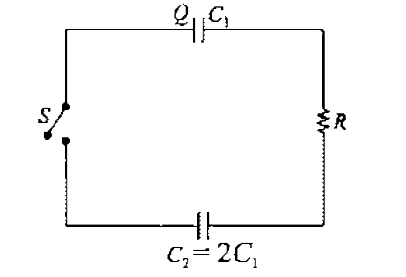
View SolutionA capacitor of capacitance C0 is charged to a potential V0 and is connected with another capacitor of capacitance C as Shown . After closing the switch S, the common potential across the two capacitors becomes V . The capacitance C is given by

View Solution