Three capacitors of capacitances 2μF,4μF and 8μF are joined in series and the combination is connected to a 12 V source. Calculate then energy stored in the combination when these are fully charged. Solution in Odia
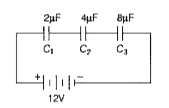
∵C1,C2 and C3 are series combination.
∴1Cs=1C1+1C2+1C3
⇒ 1C8=12+14+18=4+2+18=78⇒C8=87μF
∵ Energy stored in the combination can be given as
E=12C8(V)2=12×87×12×12×10−6
E=8.22×10−5J
Similar Questions
An infinite number of capacitors, having capacitances 1muF, 2muF, 4muF and 8muF….. are connected in series. The equivalent capacitance of the system is
View SolutionA system of 2 capacitors of capacitance 2μF and 4μF is connected in series across potential difference of 6 V. The electric charge and energy stored in the system are
View SolutionAn infinite number of capacitors having capacitances 1muF,2muF,4muF,8muF...... are connected in series. The equivalent capacitance of the system is :
View SolutionTwo capacitors of capacitances C_(1)=2muF and C_(2)=8muF are connected in series and the resulting combination is connected across a 300V battery. Calculate the charge, potential difference and energy stored in the capacitor separately.
View SolutionThree capacitors of capacitances 1μF,2μFand4μF are connected first in a series combination, and then in parallel combination. The ratio of their equivalent capacitances will be
View SolutionThree capacitors of capacitances [2muF, 3muF and 4muF] are connected in sereis. : a Find the equivalent capacitance of the combination
View SolutionThree capacitors of capacities 2muF, 4muF and 8muF are joined in series and the combination is connected to a 12V source. Calculate the energy stored in the combination when these are fully charged.
View SolutionThree capacitors of capacitis 4μF,8μFand12μF connected in series. If the charge on the 8μF capacitor is 1201μC then find the charge on each capacitor.
View Solution
