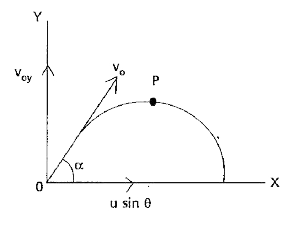
Shows that the projection angle θo for a projectile launched from the origin is given by θo=tan−1(4hmR) where the symbols have their usual meaning.Solution in Punjabi
Step by step video & image solution for Shows that the projection angle theta_o for a projectile launched from the origin is given by theta_o=tan^-1((4h_m)/R) where the symbols have their usual meaning. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A steel wire of length 4.7 m and cross-sectional area 3.0×10−5m2 stretches by the same amount as a copper wire of length 3.5 m and cross-sectional area of 4.0×10−5M2 under a given load. What is the ratio of the Young’s modulus of steel to that of copper?
View SolutionIn which of the following examples of motion, can the body be considered approximately a point object:
View SolutionShow that projection angle θ0 for a projectile launched from the origin is given by:
θ0=tan−1[4HmR] Where Hm= Maximum height, R=Range
View Solutionसिद्ध कीजिये की मूल बिंदु से फेंके एक गए प्रक्षेप्य कोण का मान tan−1(4hmR) होंगे | यहां प्रयुक्त प्रतीकों के अर्थ सामान्य है |
View SolutionShow that the projection angle theta_0 for a projectile launched from the origin is given by theta_0=tan^(-1)((4H)/R) Where the symbols have their usual meaning.
View Solution(a) Show that for a projectile the angle between the velocity and the X-axis as a function of time is given by
θ(t)=tan−1[voy−gtvox]
(b) Show that the projection angle θ0 for a projectile lunched from the origin is given by θ0=tan−1(4hmR),
where the symbols have their usual meanings .
View Solution(a) Show that for a projectile the angle between the velocity and the x - axis as a function of time is given by
θ(t)=tan−1(v0y−gtv∘x)
(b) Shows that the projection angle θ∘ for a projectile launched from the origin given by
θ0=tan−1(4hmR)
where the symbols have their usual meaning.
View Solution(a) Show that for a projectile the angle between the velocity and the x - axis as a function of time is given by
θ(t)=tan−1(v0y−gtv∘x)
(b) Shows that the projection angle θ∘ for a projectile launched from the origin given by
θ0=tan−1(4hmR)
where the symbols have their usual meaning.
View Solution(a) Show that for a projectile the angle between the velocity and the x - axis as a function of time is given by
θ(t)=tan−1(v0y−gtv∘x)
(b) Shows that the projection angle θ∘ for a projectile launched from the origin given by
θ0=tan−1(4hmR)
where the symbols have their usual meaning.
View SolutionShow that for a projectile the angle between the velocity and the x-axis as function of time is given
by θt=tan−1(v0y−gtvox)
(b) Shows that the projection angle θ0 for a projectile launched from the origin is given by θt=tan−1(4hmR)
where the symbols have their usual meanings.
View SolutionProve that, projectile from the origin theta_(0) Projection angle when projected at projection angle theta_(0)=tan^(-1)[(4H_(m))/(R)] it happens. Where H_(m) = Maximum height, R = Horizontal range
View SolutionShow that a + r +1=1 where symbols have their usual meaning.
View SolutionShow that projection angle θ0 for a projectile launched from the origin is given by:
θ0=tan−1[4HmR] Where Hm= Maximum height, R=Range
View SolutionShow that the projection angle θ for a projectile launched from the origin is given y θ(t)=tan−1[υ∘0y−gtυ0x]
θ0=tan−1(4hmR) where the symbols have their usual meaning.
View SolutionShow that the projection angle thetha_0 for a projectile launched from the origin is given by theta_0 =tan^1(4h_m//R) Where the symbols have their usual meaning.
View Solution
