A wire of length 28 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the length of the two pieces so that the combined area of the square and the circle is minimum?
Let r be the radius of the circle and x be the side of square.
∴ Circumference of circle + perimeter of square = 28 cm
⇒2πr+4x=28
⇒x=14−πr2 ….(1)
and let area of circle + area of square = A
∴A=πr2+x2
=πr2+(14−πr2)2 [From equation (1)]
=πr2+14(π2r2−28πr+196)
⇒dAdr=2πr+14(2π2r−28π)
and d2Adr2=2π+14(2π2)
For maxima/minima dAdr=0
⇒πr+14(2π2r−28π)=0
⇒πr+π2r−14π=0
⇒r(4+π)=14
⇒r=14π+4
at r=14π+4
d2Aπr2>0
⇒ A is minimum.
Now 2πr=2π(14π+4)=28ππ+4
and 4x=28−2πr
=28−28ππ+4=112π+4
Therefore, the length of two pieces of wire =28ππ+4cmand112π+4 cm.
Topper's Solved these Questions
- APPLICATIONS OF DERIVATIVESBook:NAGEEN PRAKASHAN ENGLISHChapter:APPLICATIONS OF DERIVATIVESExercise:Miscellaneous Exercise
Explore 24 Videos
- APPLICATIONS OF DERIVATIVESBook:NAGEEN PRAKASHAN ENGLISHChapter:APPLICATIONS OF DERIVATIVESExercise:Exercise 6.4
Explore 9 Videos
- APPLICATIONS OF INTEGRALSBook:NAGEEN PRAKASHAN ENGLISHChapter:APPLICATIONS OF INTEGRALSExercise:Miscellaneous Exercise
Explore 19 Videos
Similar Questions
A wire of length 36m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the lengths of the two pieces, so that the combined area of the square and the circle is minimum?
View SolutionA wire of length 36m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the lengths of the two pieces, so that the combined area of the square and the circle is minimum?
View Solution
Knowledge Check
The side length of a square inscribed in a circle is 2. what is the area of the circle?
AπB√2πC2πD2√2π
A wire of length 20m is to be cut into two pieces. One of the places will be bent into shape of a square and the other shape of an equilateral triangle. Where the wire should be cut so that the sum of the areas of the square and triangle is minimum?
View SolutionA wire of length 1212m is cut into 10 pieces of equal length. Find the length of each piece.
View SolutionA wire of length l is cut into two parts. One part is bent into a circle and the other into a square. Prove that the sum of the areas of the circle and the square is the least, if the radius of the circle is half of the side of the square.
View SolutionA cable o f length 257 14 m has to be cut into 21 pieces o f equal length. Fin d the length o f each piece.
View SolutionA square is bisected into two triangles (see figure). If the length of BD is 16√2 inches, what is the area of the square?
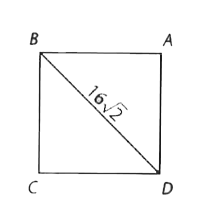
View SolutionA wire of length 2 units is cut into two parts which are bent respectively to from a square ofside c units and a circle of radius r units if the sum of the sum of the areas of the square and the circle so fromed is minimum then
View SolutionA wire of length I is cut into three pleces. What Is the probability that the three pieces form a triangle ?
View Solution

