Question

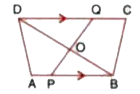
In the given figure $△ACB~△APQ$. If BC= 8cm , PQ = 4cm BA= 6.5 cm, AP = 2.8 cm, find CA and AQ.

Explanation

To solve the problem, we will use the property of similar triangles, which states that the corresponding sides of similar triangles are in proportion.

1. Identify the Similar Triangles: We know that triangle ACB is similar to triangle APQ. This gives us the relationship between the sides of the triangles.

2. Write the Proportions: From the similarity of the triangles, we can set up the following proportions:
\( \frac{AC}{AP} = \frac{BC}{PQ} \quad \text{and} \quad \frac{AB}{AQ} = \frac{BC}{PQ} \)

3. Substitute Known Values: We know the following values:
- \( BC = 8 \, \text{cm} \)
- \( PQ = 4 \, \text{cm} \)
- \( BA = 6.5 \, \text{cm} \)
- \( AP = 2.8 \, \text{cm} \)

Using the first proportion:
\( \frac{AC}{2.8} = \frac{8}{4} \)

4. Simplify the Proportion: The ratio \( \frac{8}{4} \) simplifies to \( 2 \):
\( \frac{AC}{2.8} = 2 \)

5. Cross-Multiply to Solve for AC:
\( AC = 2 \times 2.8 = 5.6 \, \text{cm} \)

6. Find AQ Using the Second Proportion: Now we will use the second proportion:
\( \frac{AB}{AQ} = \frac{BC}{PQ} \)
Substituting the known values:
\( \frac{6.5}{AQ} = \frac{8}{4} \)

7. Simplify the Proportion: Again, \( \frac{8}{4} \) simplifies to \( 2 \):
\( \frac{6.5}{AQ} = 2 \)

8. Cross-Multiply to Solve for AQ:
\( 6.5 = 2 \times AQ \implies AQ = \frac{6.5}{2} = 3.25 \, \text{cm} \)

Final Answers:
- \( AC = 5.6 \, \text{cm} \)
- \( AQ = 3.25 \, \text{cm} \)