In the adjoining figure, D,E and F are the mid- points of the sides of ΔPQR and 'S' is the fooot of perpendicualar form P to side S.
Prove that:
(i) FQ=FS and ∠FQS=∠FSQ.
(ii)∠FQS=∠FED.
(iii) square FSDE is a cyclic quadrilateral.
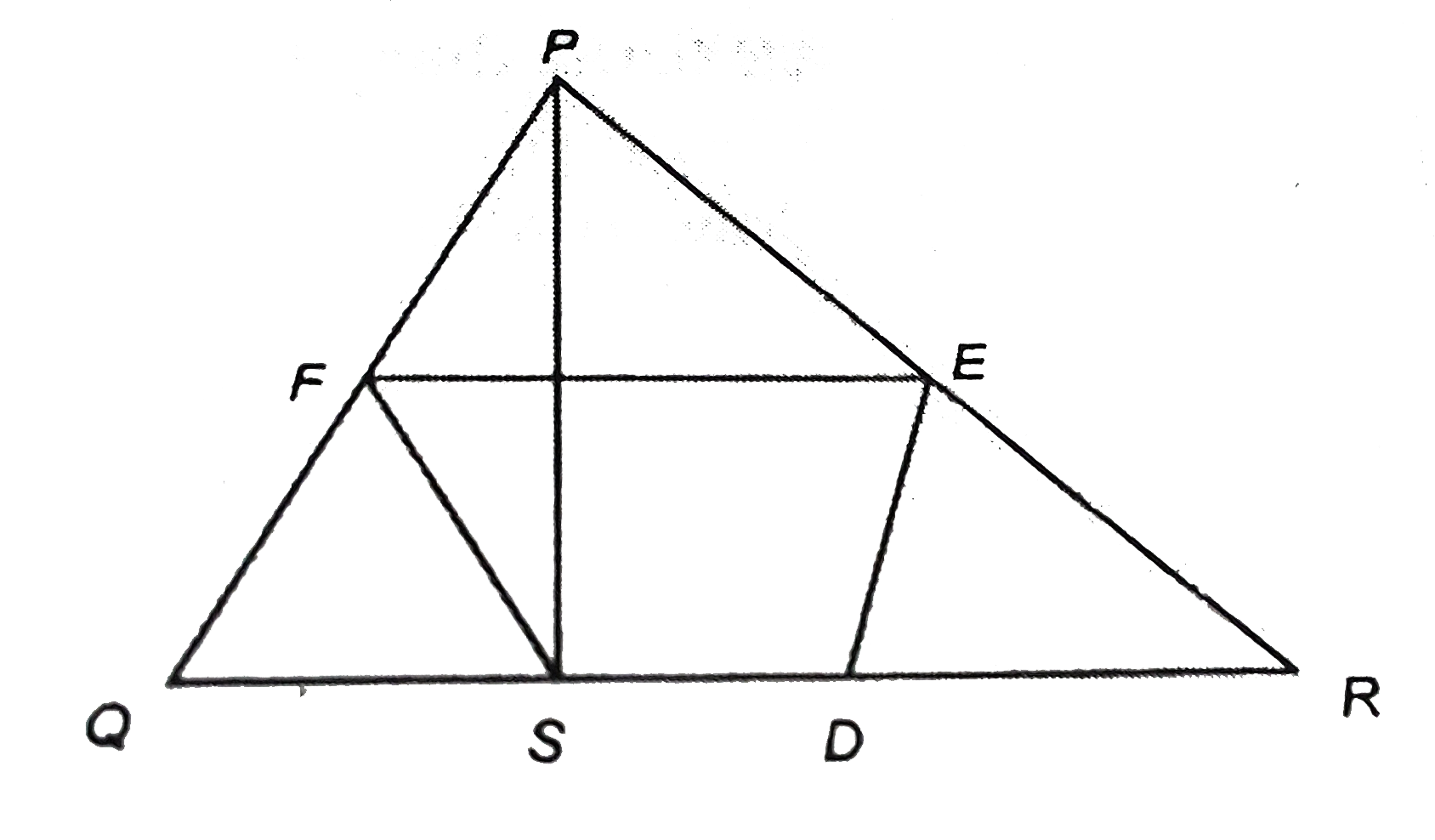
(i) PS⊥QR
⇒∠PSQ=90∘
F is the mid-point of PQ.
∴FS=12PQ or FS=FP
Now, ΔPQS is right-angled triangle and we know that the mid-point of hypotenuse is equidistant form the vertices of a triangle.
∴FQ=FP=FS
⇒FQ=FS
⇒∠FSQ=∠FQS ..........(1)
(ii) F is the mid-point of PQ and E is the mid-point of PR.
∴FE| |QR
⇒FE| |QD
Similarly, FQ| |ED
∴□FEDQ is a parallelogram.
We know that opposite angles of a parallelogram are equal.
∴∠FQS=∠FED
(iii) Now from eqs. (1) and (2),
∠FSQ=∠FED
But ∠FSQ is the exterior angle of square FSDE.
square FSDE is a cyclic quadrilateral.
Topper's Solved these Questions
- CIRCLE Book:NAGEEN PRAKASHAN ENGLISHChapter:CIRCLE Exercise:Exercise 10a
Explore 22 Videos
- CIRCLE Book:NAGEEN PRAKASHAN ENGLISHChapter:CIRCLE Exercise:Exercise 10b
Explore 19 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBook:NAGEEN PRAKASHAN ENGLISHChapter:AREA OF PARALLELOGRAMS AND TRIANGLESExercise:Revision Exercise (long Answer Question)
Explore 5 Videos
- CO-ORDINATE GEOMETRY Book:NAGEEN PRAKASHAN ENGLISHChapter:CO-ORDINATE GEOMETRY Exercise:Exercise
Explore 8 Videos
Similar Questions
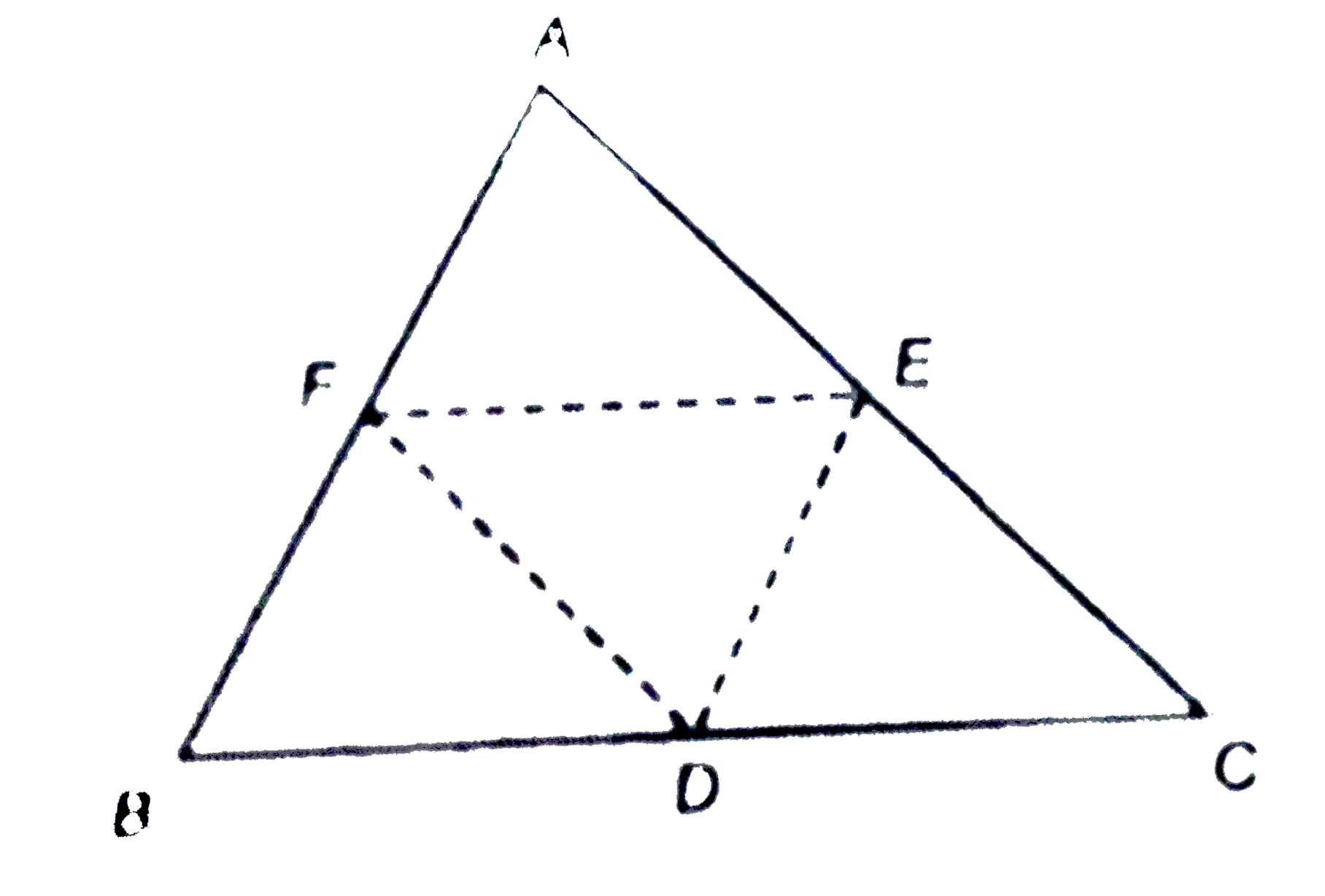
In the adjoining figure D, E and F are the mid-points of the sides BC, CA and AB of the equilateral ΔABC. Prove that ΔDEF is also an equilateral triangle.

View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, CA and AB respectively of ΔABC. Prove that:
(i) □BDEF is a parallelogram
(ii) area of ΔDEF=14× area of ΔABC
(iii) □BDEF=12× area of ΔABC
View SolutionIn Figure, D,E and F are, respectively the mid-points of sides BC,CA and AB of an equilateral triangle ABC . Prove that DEF is also an equilateral triangle.
View SolutionIn Figure, D,E and F are, respectively the mid-points of sides BC,CA and AB of an equilateral triangle ABC . Prove that DEF is also an equilateral triangle.
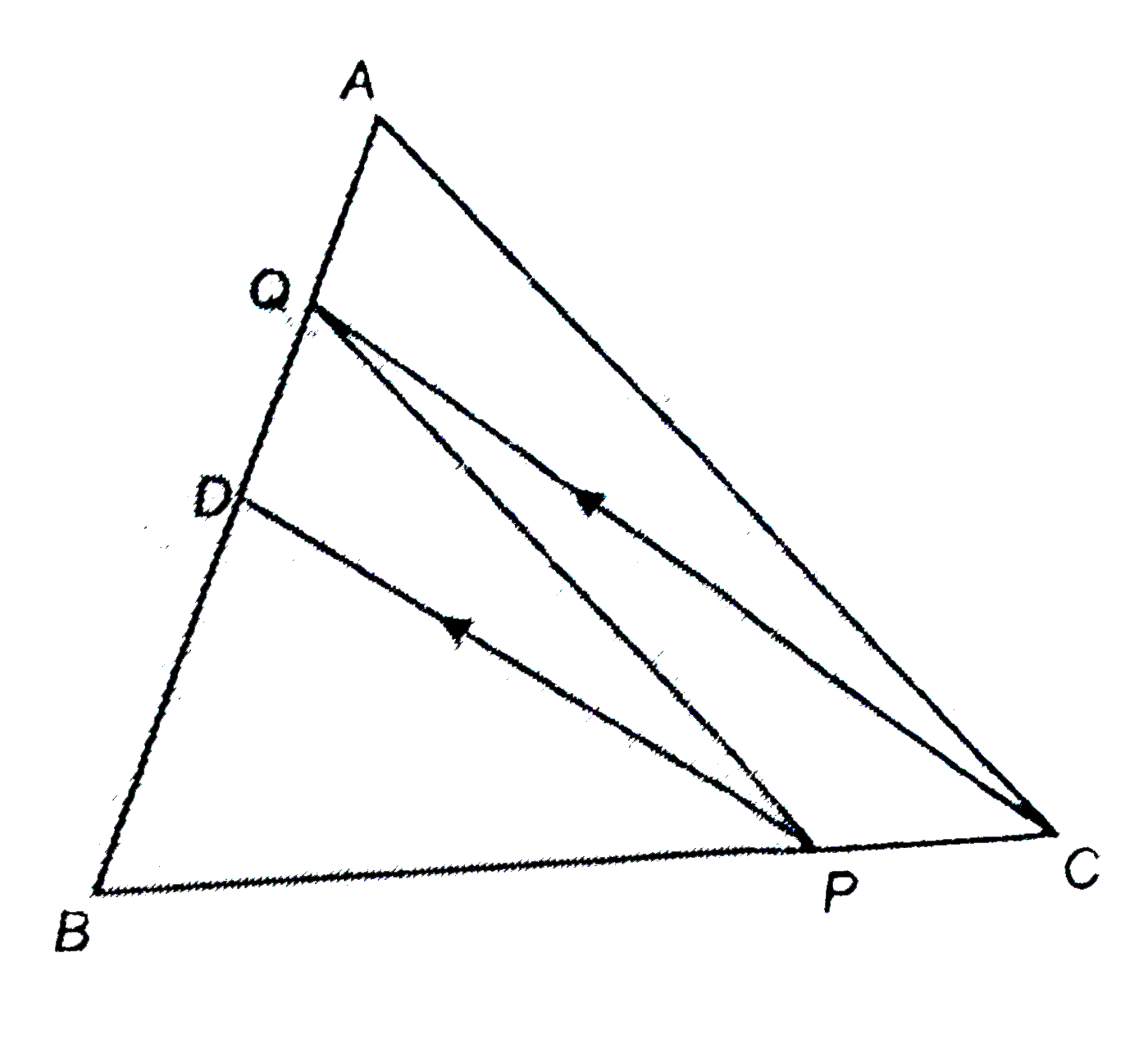
View SolutionIn the adjoining figure, D is the mid-point of side AB of ΔABC and P be any point on side BC. If CQ∣∣PD, then prove that:
area of ΔBPQ=12× area of ΔABC
View SolutionIf D,E and F are the mid-points of the sides BC,CA and AB, respectively of a ΔABC and O is any point, show that
(i) AD+BE+CF=0
(ii) OE+OF+DO=OA
View SolutionP, Q , R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
View SolutionP, Q, R and S are respectively the mid-points of sides AB, BC, CD and DA of quadrilateral ABCD in which AC=BD and AC⊥BD. Prove that PQRS is a square.
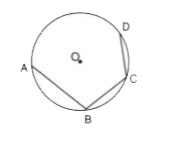
View SolutionIn the given figures , O is the centre of the given circle. AB is a side of a square ,BC
is a side of regular pentagon and CD is a side of regular hexagon. Find:
(i) ∠AOB
(ii) ∠AOC
(iii) ∠AOD
(iv)∠BCD
View SolutionD, E and F are the mid-points of the sides AB, BC and CA respectively of A ABC. AE meets DF at O. P and Q are the mid-points of OB and OC respectively. Prove that DPOF is a parallelogram.
View Solution

