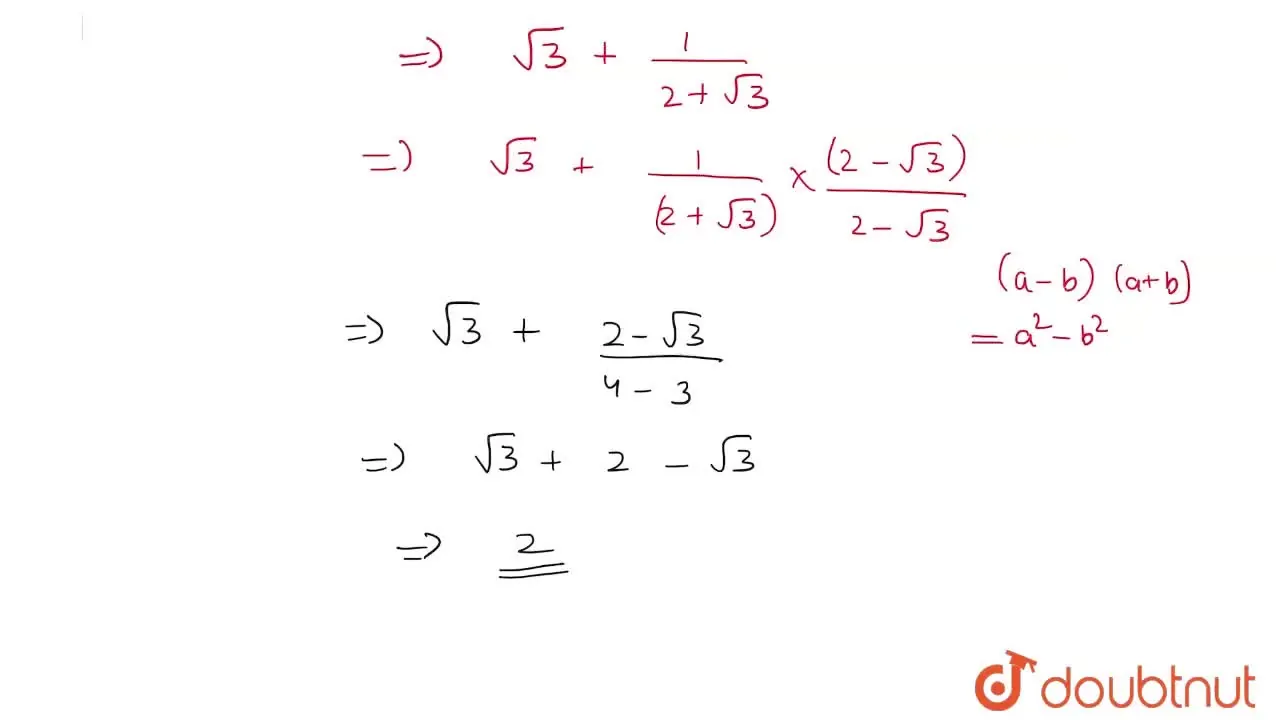If sec A= 2, then find the value of 1cotA+cosA1+sinA
Video Solution
Text Solution
Given that , secA=2=21
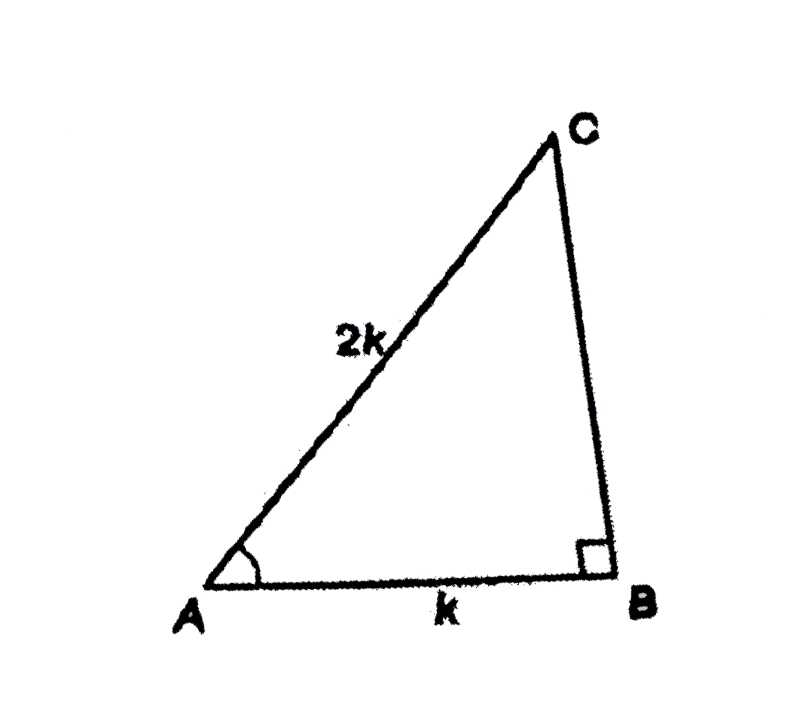
Construct a right - angled ΔABC in which
∠ABC=90∘,AB=kandAC=2k.
In ΔABC,
From Pythagoeas theorem
AB2+BC2=AC2
⇒BC2=AC2−AB2=(2k)2−(k)2=4k2−k2=3k2
⇒BC=√3k
Now , cotA=ABBC=k√3k=1√3
sinA=BCAC=√3k2k=√32andcosA=ABAC=k2k=12
∴1cotA+cosA1+sinA=11√3+121+√32=√3+122+√32
=√3+1×(2−√3)(2+√3)(2−√3)=√3+2−√34−3
√3+2−√3=2
|
Updated on:21/07/2023
Related Playlists
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - Problems From NCERT/exemplar29videos
INTRODUCTION TO TRIGONOMETRY
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - Exercise 8a20videos
INTRODUCTION TO TRIGONOMETRY
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Exercise 11 B10videos
CONSTRUCTIONS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - Revision Exercise Long Answer Questions8videos
LINEAR EQUATIONS IN TWO VARIABLES
Similar Questions
If cosecA=2, find the value of 1tanA+sinA1+cosA
View SolutionIf cosec A=2 , find the value of 1tanA+sinA1+cosA
View SolutionIf A lies in the second quadrant and 3tanA+4=0, then find the value of 2cotA−5cosA+sinA.
View SolutionIf sinA=cosA,then find the value of sin 2A.
View SolutionIf tanA=1
then find the value of , (cosA+sinA)2=?View SolutionIf cosA=725 , find the value of tanA+cotA .
View SolutionIf tanA=1,then find the value of sin2A+cos2A+cotA.
View SolutionGiven that 16cotA=12 ; find the value of sinA+cosAsinA−cosA .
View SolutionIf A lies in the second quadrant and 3tanA+4=0, then the value of 2cotA−5cosA+sinA is
View SolutionIf tanA=512, find the value of (sinA+cosA)secA .
View Solution