In the adjoining figure, AB is a chord of length 9.6 cm of a circle with centre O and radius 6 cm. The tangents at A and B intersect at P. Find the length of PA.
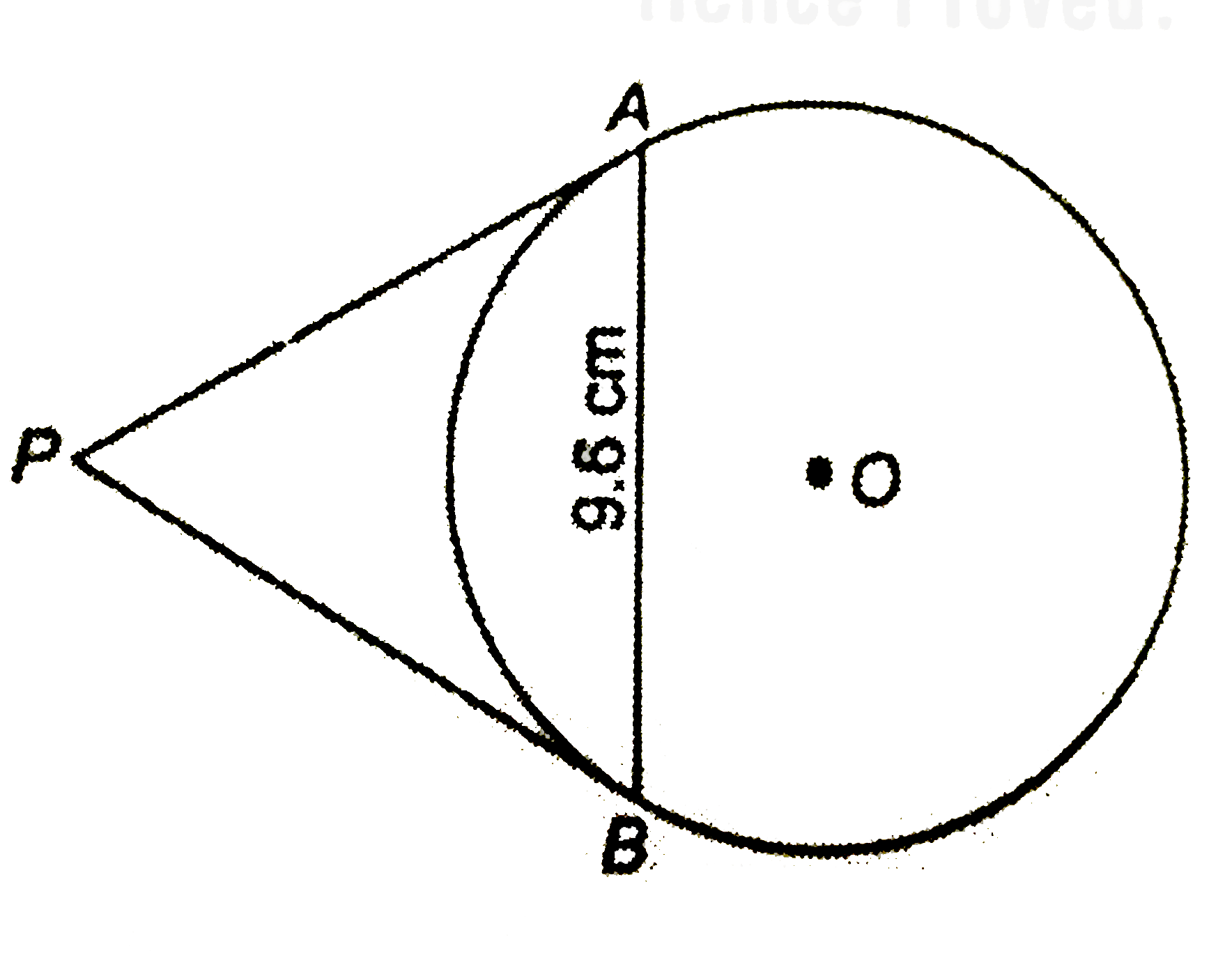
Join OP,OA and OB.
Let PA=xcm and PM=ycm
In △APM and △BPM
∵ ⎧⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪⎩PA=PB (length of tangents from an external point are equal)PM=PM (common)∠1=∠2 (tangents are equally inclined at the centre)
∴ △AMP≅△BPM (SAS congruency)
∴ AM=MB=9.62=4.8cm (c.p.c.t)
and ∠PMA=∠PMB (c.p.c.t)
But ∠PMA+∠PMB=180∘ (L.P.A)
∴ ∠PMA=∠PMB=90∘
Now, in right △AMP,
x2=y2+(4.8)2 (by Pythagoras theorem)
.....(1)
Also, in right △AMO,
(4.8)2+OM2=(6)2
∴ OM2=36−23.04=12.96
∴ OM=√12.96=3.6cm
Now ∠OAP=90∘ (radius through point of contact is ⊥ to the tangent)
In right △AOP,
OP2=OA2+AP2
⇒ (y+3.6)2=36+x2
⇒y2+12.96+7.2y=36+y2+(4.8)2 [from (1)]
⇒ 7.2y=36+23.04−12.96 ⇒ 7.2y=46.08
⇒ y=46.087.2=6.4cm
Put this value of y in equation (1),
∴ x2=(6.4)2+(4.8)2=40.96+23.04=64
∴ x=8cm
Hence, x=8cm and y=6.4cm

Topper's Solved these Questions
- CIRCLESBook:NAGEEN PRAKASHAN ENGLISHChapter:CIRCLESExercise:Problems From NCERT/exemplar
Explore 11 Videos
- CIRCLESBook:NAGEEN PRAKASHAN ENGLISHChapter:CIRCLESExercise:Exercise
Explore 32 Videos
- ARITHMETIC PROGRESSIONBook:NAGEEN PRAKASHAN ENGLISHChapter:ARITHMETIC PROGRESSIONExercise:Revision Exercise Long Answer Question
Explore 5 Videos
- CO-ORDINATE GEOMETRYBook:NAGEEN PRAKASHAN ENGLISHChapter:CO-ORDINATE GEOMETRYExercise:Revision Exercise Short Answer Questions
Explore 10 Videos
Similar Questions
AB is a chord of length 16cm of a circle of radius 10cm. The tangents at A and B intersect at a point P . Find the length of PA .
View SolutionPQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T . Find the length TP .
View SolutionPQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T (see Fig. 10.10). Find the length TP.
View SolutionIn a circle with centre O and radius 5cm, AB is a chord of length 5√3cm . Find the area of sector AOB.
View SolutionAB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm and divides the circle into two segments. Find the area of the minor segment.
View SolutionAB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm. Find the area of sector of the circle formed by chord AB .
View SolutionIn the adjoining figure, AB=8cm,DM=6cmandBC=6cm. Find the length of DN

View SolutionIn the adjoining figure ,AB and CD are two parallel chords of a circle with centre O , whose length are 16 cm and 12 cm respectively. Find the radius of the circle if the distance between them is 14 cm.
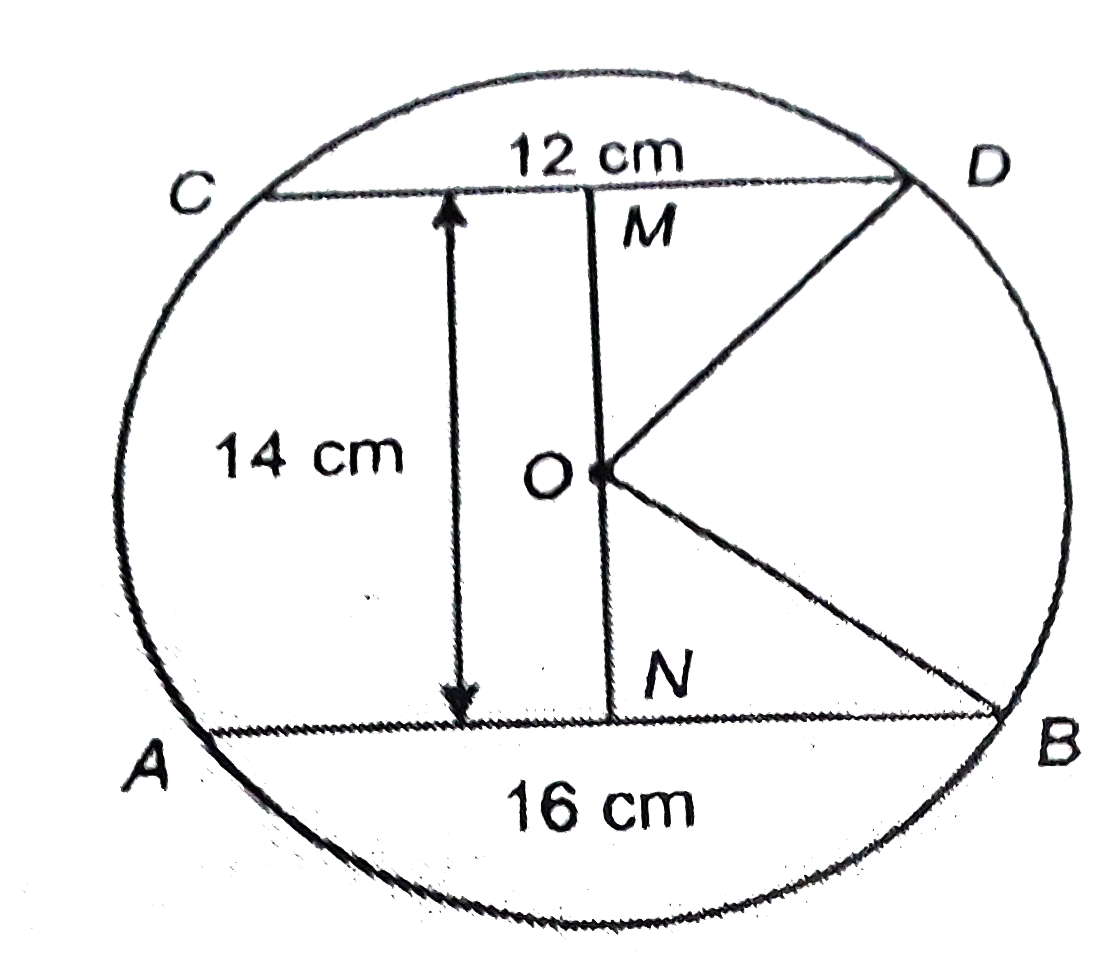
View SolutionIn the adjoining figure O is the centre of the circle . If chord AB=2 cm radius OA=2 cm, then find the value of ∠ACB.

View SolutionGiven a circle with centre O and radius 2.5 cm, what is the length of the longest chord of the circle
View Solution

