AB is a diameter of a circle. AHandBK are perpendiculars from A and B respectively to the tangent at P Prove that AH+BK=AB.
Let AH=x,BK=yandBM=z
△MBK~△MAH (AA corollary)
∴ BKAH=BMAM ⇒ yx=z2r+z
∴ 2ry+yz=xz ⇒ z(x−y)=2ry
⇒ z=2ryx−y ...(1)
Similarly,
ΔMBK~ΔMOP (AA corollary)
∴ BKOP=BMOM ⇒ yr=zz+r
⇒ yz+yr=zr
⇒ z(r−y)=yr
⇒ z=yrr−y ...(2)
From (1) and (2), we get
2ryx−y=yrr−y ⇒ 2x−y=1r−y
⇒ 2r−2y=x−y
⇒ x+y=2r
AH+BK=AB Hence Proved.
Topper's Solved these Questions
- CIRCLESBook:NAGEEN PRAKASHAN ENGLISHChapter:CIRCLESExercise:Problems From NCERT/exemplar
Explore 11 Videos
- CIRCLESBook:NAGEEN PRAKASHAN ENGLISHChapter:CIRCLESExercise:Exercise
Explore 32 Videos
- ARITHMETIC PROGRESSIONBook:NAGEEN PRAKASHAN ENGLISHChapter:ARITHMETIC PROGRESSIONExercise:Revision Exercise Long Answer Question
Explore 5 Videos
- CO-ORDINATE GEOMETRYBook:NAGEEN PRAKASHAN ENGLISHChapter:CO-ORDINATE GEOMETRYExercise:Revision Exercise Short Answer Questions
Explore 10 Videos
Similar Questions
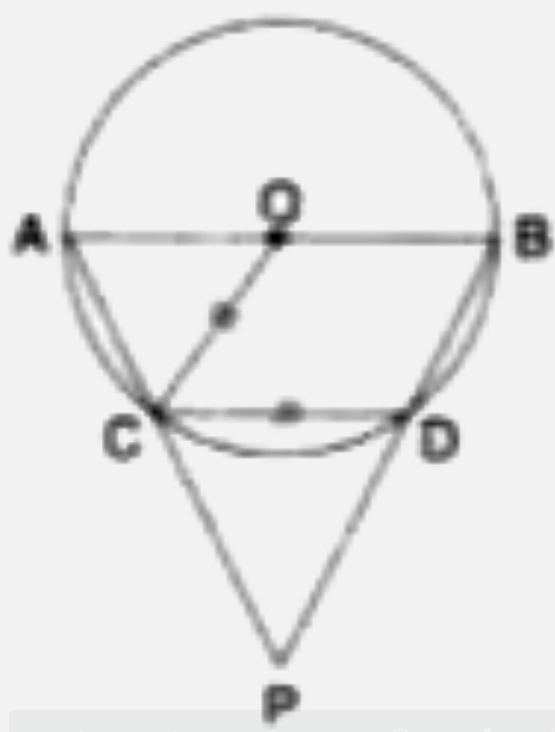
AB is a diameter of a circle with centre O. Chord CD is equal to radius OC. AC and BD produced intersect at P. Prove that : ∠APB=60∘
View SolutionAB is a diameter of a circle. CD is a chord parallel to AB and 2CD=AB. The tangent at B meets the line AC produced at E then AE is equal to -
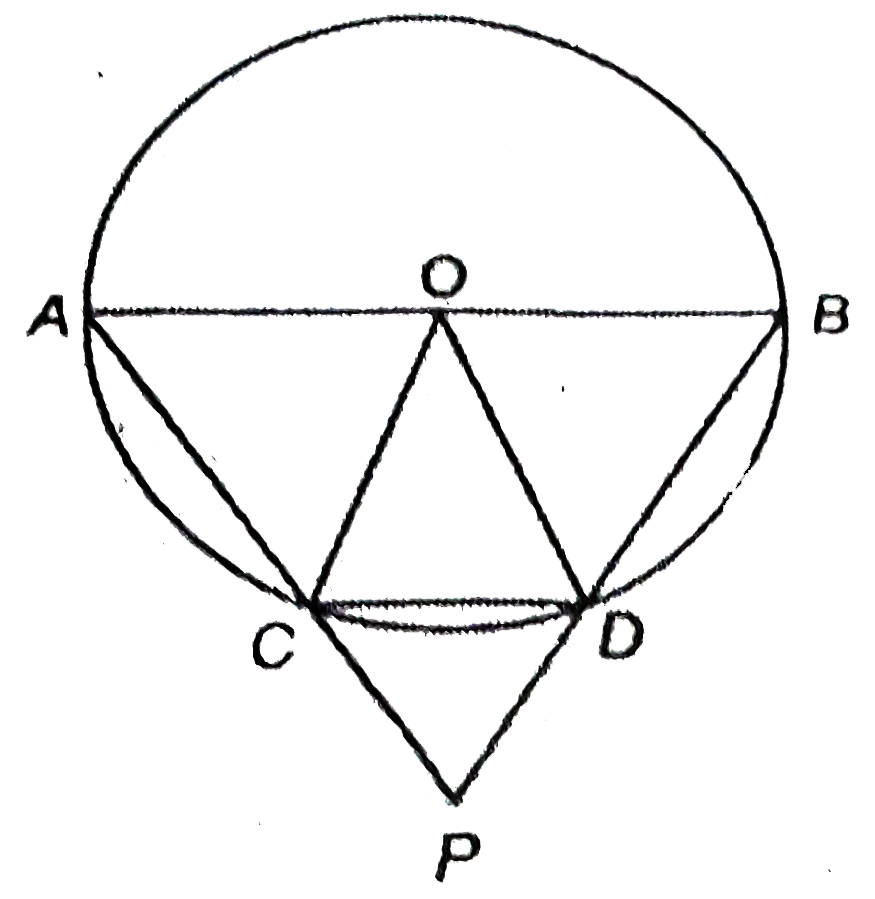
View SolutionAB is a diameter of the circle with centre O and chord CD is equal to radius OC (fig). AC and BD proudced meet at P. Prove that ∠CPD=60∘.
View SolutionTwo circle intersect in A and B and AC and AD are respectively the diameters of the circles. Prove that C,B,D are collinear.
View SolutionProve that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
View SolutionIn a triangle ABC , let P and Q be points on AB and AC respectively such that PQ∣∣BC . Prove that the median AD bisects PQ.
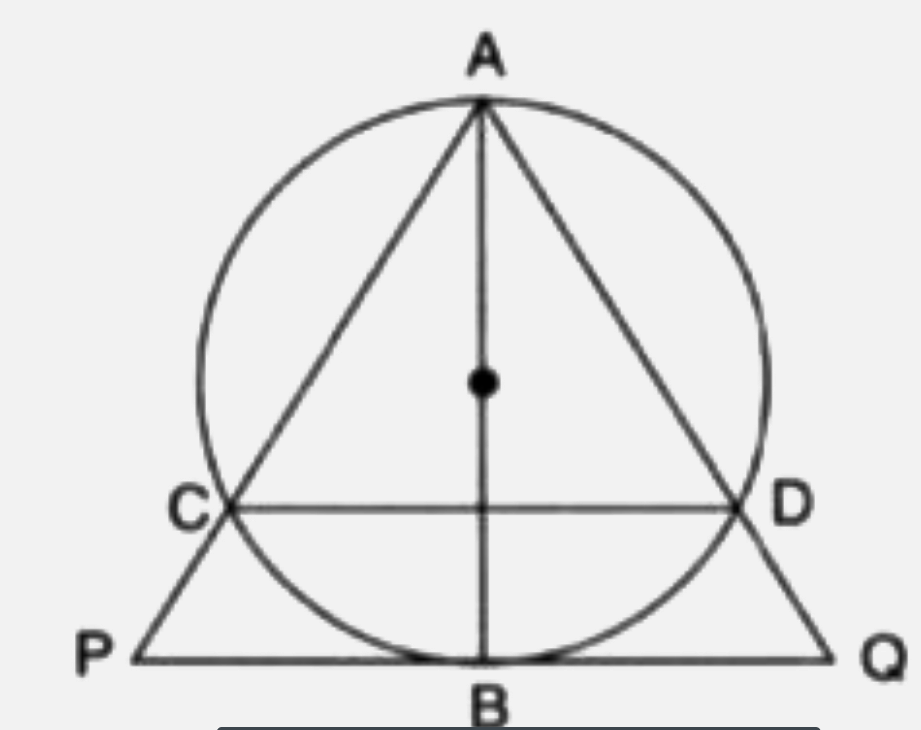
View SolutionThe given figure shows, AB is a diameter of the circle. Chords AC and AD produced meet the tangent to the circle at point B in points P and Q respectively. Prove that:
AB2=AC×AP
View SolutionAB is the diameter of a circle with centre O. A line PQ touches the given circle at point R and cuts the tangents to the circle through A and B at points P and Q respectively. Prove that ∠POQ=90∘
View SolutionLet ABC be an acute angled triangle with orthocenter H.D, E, and F are the feet of perpendicular from A,B, and C, respectively, on opposite sides. Also, let R be the circumradius of ΔABC. Given AH.BH.CH=3and(AH)2+(BH)2+(CH)2=7
Then answer the following
Value of R is
View SolutionAD is a diameter of a circle and AB is a chord. If AD = 34cm, AB = 30cm, the distance of AB form the centre of the circle is
View Solution

