Find the mean number of heads in three tosses of a fair coin.
The correct Answer is:N/a
Probability of getting head or tail in a toss of one coin is
P(H)=P(T)=12
Sample space in three throw of an unbiased coin is
S={HH,HHT,HTH,THH,THT,TTH,HTT,TTT}
The possible values of random variable X are 0,1,2 or 3.
∴P(X=0)=P (getting all tails)
=P{TTT}=12×12×12=18
P(X=1)=P (getting one head and two tails)
=P(TTH)+P(THT)+P(HTT)
=12×12×12+12×12×12+12×12×12
=18+18+18=38
P(X=2)=P (getting two heads and one tail)
P(HHT)+P(HTH)+P(THH)
=12×12×12+12×12×12+12×12×12
=18+18+18=38
P(X=3)=P (gettting three heads)
=P(HHH)=12×12×12=18
Therefore the required probability distribution is:
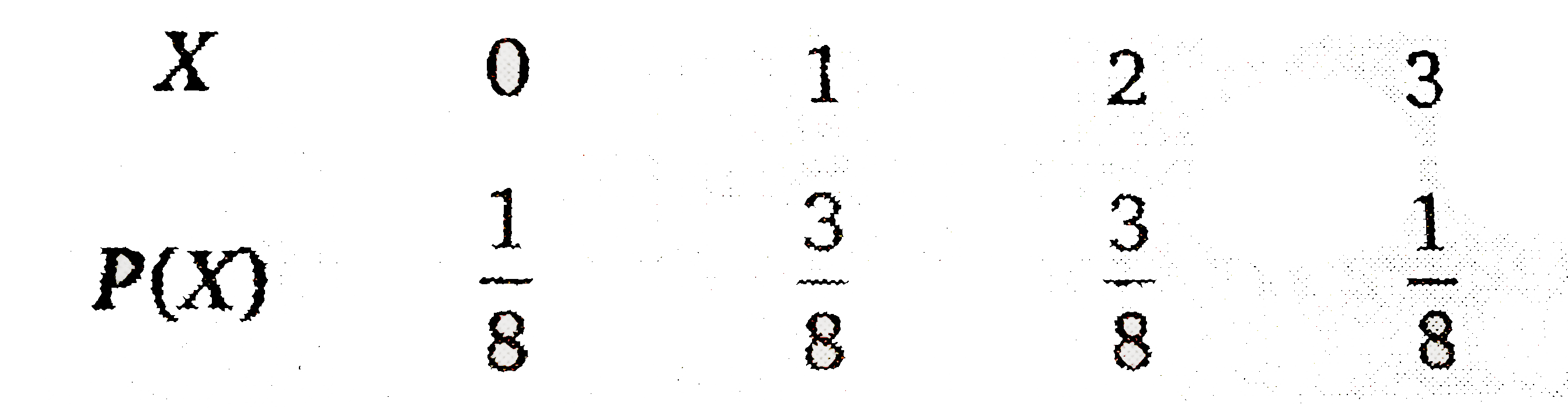
Therefore mean
=∑XP(X)=0×18+1×38+2×38+3×18
=38+68+38=128=32=1.5
Topper's Solved these Questions
- PROBABIILITYBook:NAGEEN PRAKASHAN ENGLISHChapter:PROBABIILITYExercise:Exercise 13.5
Explore 15 Videos
- PROBABIILITYBook:NAGEEN PRAKASHAN ENGLISHChapter:PROBABIILITYExercise:Miscellaneous Exercise
Explore 19 Videos
- PROBABIILITYBook:NAGEEN PRAKASHAN ENGLISHChapter:PROBABIILITYExercise:Exercise 13.3
Explore 14 Videos
- MATRICESBook:NAGEEN PRAKASHAN ENGLISHChapter:MATRICESExercise:Miscellaneous Exerice
Explore 15 Videos
- RELATIONS AND FUNCTIONS Book:NAGEEN PRAKASHAN ENGLISHChapter:RELATIONS AND FUNCTIONS Exercise:Miscellaneous Exercise
Explore 19 Videos
Similar Questions
Find the mean and variance of the number of heads in the two tosses of a coin.
View SolutionFind the probability distribution for number of heads obtained in three tosses of a coin.
View SolutionFind the expectation of the number of heads in 15 tosses of a coin.
View SolutionFind the probability distribution of (i) number of heads in two tosses of a coin. (ii) number of tails in the simultaneous tosses of three coins. (iii) number of heads in four tosses of a coin.
View SolutionFind the probability distribution of X; the number of heads in two tosses of a coin ( or a simultaneous toss of two coins).
View SolutionFind the probability distribution for number of heads obtained in two tosses of a coin.
View SolutionFind the mean, variance and standard deviation of the number of heads in a simultaneous toss of three coins.
View SolutionFind the probability distribution of the number of heads when three coins are tossed.
View SolutionFind the probability distribution of the number of heads when three coins are tossed.
View SolutionFind the probability of getting two heads in two tosses of a coin.
View Solution