A coin is biased so that the head is 3 times as likely to occur as tail. If the coin is tossed twice, find the probability distribution of number of tails.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:N/a

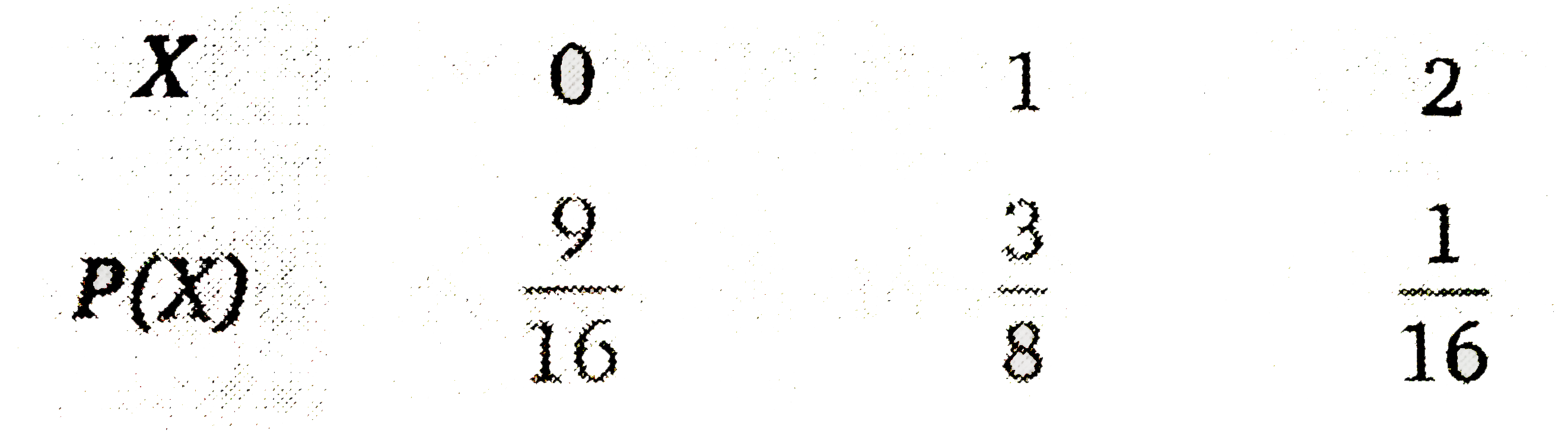
Let $X$ be a random variable which represents the number of tails in two throws of a biased coin. Therefore the possible values of $X$ are 0,1 or 2.
Since coin is biased in which the possibility of getting head is three times are possbility of getting tail.
$∴ P ({H}) = \frac{3}{4}$ and $P ({T}) = \frac{1}{4}$
$P (X = 0) = P ({HH}) = {(\frac{3}{4})}^{2} = \frac{9}{16}$
$P (X = 1) = P$ (a tail and a head)
$= P ({H T, T H} = P ({H T}) + P {(T H})$
$= P ({H}) P ({T}) + P ({T}) P ({H})$
$= \frac{3}{4} \times \frac{1}{4} + \frac{1}{4} \times \frac{3}{4} = \frac{3}{16} + \frac{3}{16} = \frac{6}{16} = \frac{3}{8}$
$P (X = 2) = P$ (two tails) $= P ({TT}) = P ({T}) . P ({T})$
$= {(\frac{1}{4})}^{2} = \frac{1}{16}$
Therefore required probability distribution is:

Updated on:21/07/2023

|

Class 12 MATHS PROBABILITY

Topper's Solved these Questions

Similar Questions

Knowledge Check

A coin is tossed twice. The probability of getting atleast one tail is
A $\frac{1}{4}$
B $\frac{3}{4}$
C $\frac{1}{2}$
D $\frac{3}{2}$

NAGEEN PRAKASHAN ENGLISH-PROBABIILITY-Exercise 13.4

Home
Ask Doubt
Profile