Question

Solve the following linear programming problem graphically:
Minimize : $z=100x+50y$
Subject to constraints $:x+2y\ge 10$
$3x+4y\ge 24$
$x\ge 0$
$y\ge 0$

Explanation

Draw the graph of equations `x+2y=10` and `3x+4y=24`.
Now obtain the feasible region for the inequalities `x+2yge10,3x+4yge24,xge0,yge0` and shade this region. The vertices of this shaded region are `A(10,0),B(4,3),` and `C(0,6)`

Now we will find the value of `z=100x+50y` at each vertex.

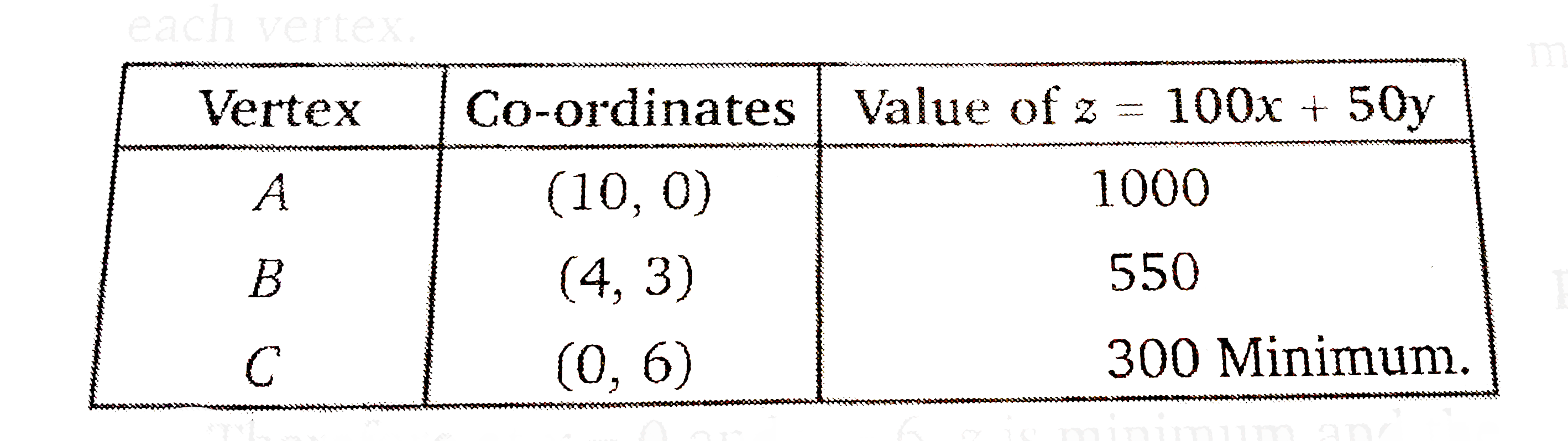
Therefore at `x=0` and `y=6,z` is minimum and the minimum value is `300`.