An aeroplane can carry a maximum of two passengers. A profit of Rs. 1000 is made on each executive clas ticket and a profit of Rs. 600 is made on each economy class ticket. The airline reserves at least 20 seats for executive class. However at least 4 times as many passengers prefer to travel by economy clas than by the executive class. Determine how many tickets of each type must be sold in order to maximise the profit for the airline. What is the maximum profit?
Let x passengers are of executive class and y passengers are of economy class.
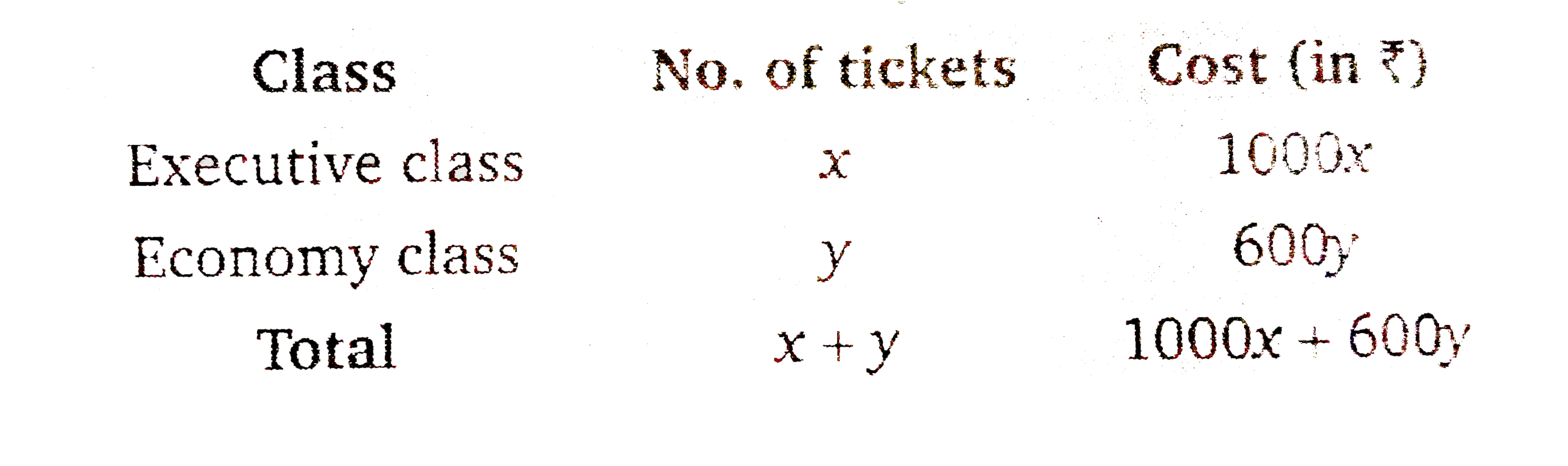
Maximise Z=1000x+600y……………1
and constraints x+y≤200………………2
x≥20…………….3
y−4x≥0⇒y≥4x…………..4
x≥0,y≥0............5
First draw the graph of the line x+y=200.
Put (0,0) in the inequation x+y≤200,
0+0≤200⇒0≤200. (True)
Thus, half plane contains the origin.
Now, draw the graph of line y=4x
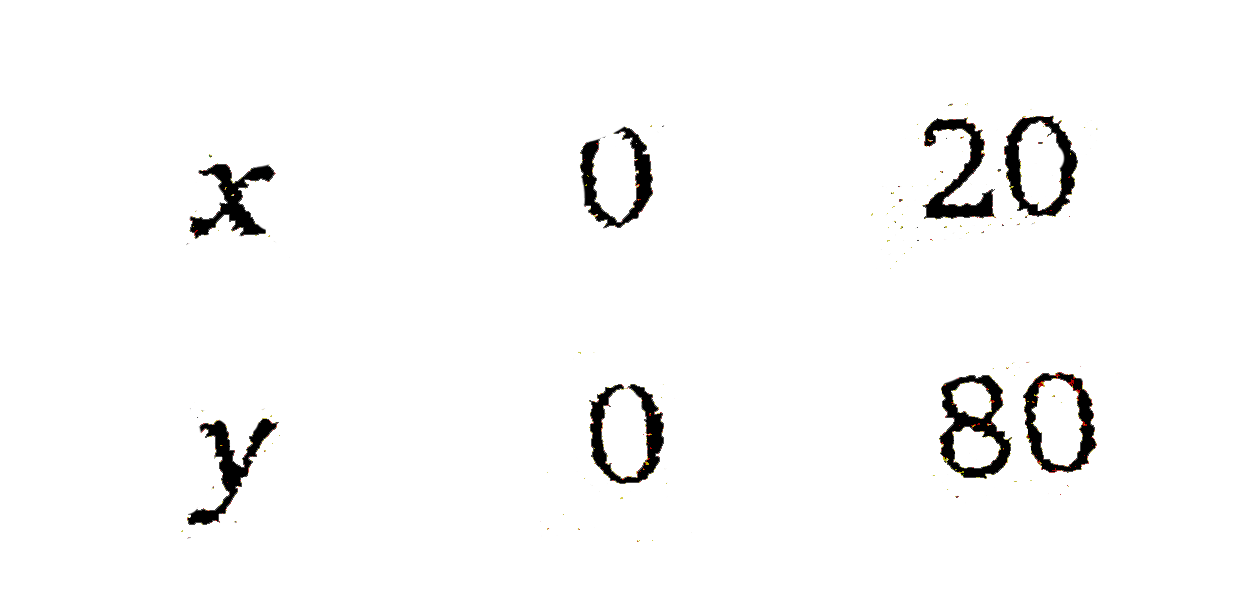
Put (10,0) in the inequation y≥4x,
0≥4×10⇒0≥40 (False)
Thus, half plane will be opposite to (10,0).
Now draw the graph of line x=20
Put (0,0) in the inequation x≥0,0≥20 (False)
Thus, the half plane does not contain origin.
Since x,y≥0, So the feasible region will be in first quadrant.
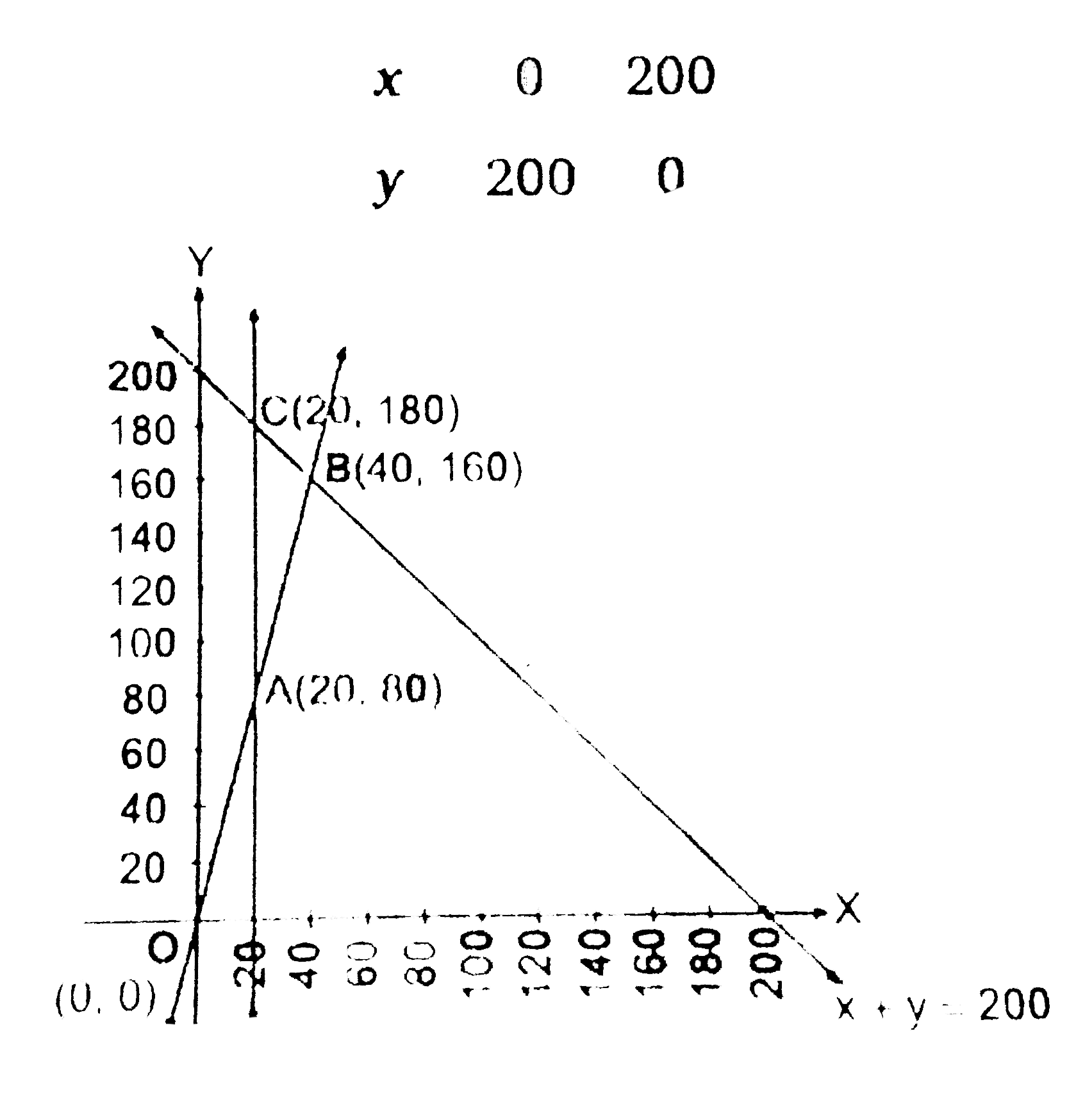
From the equations the points of intersection are A(20,80),B(40,160) and C(20,180).
∴ Feasible region is ABCA
The vertices of the feasible region are A(20,80),B(40,160) and C(20,180) at which we find the value of Z.
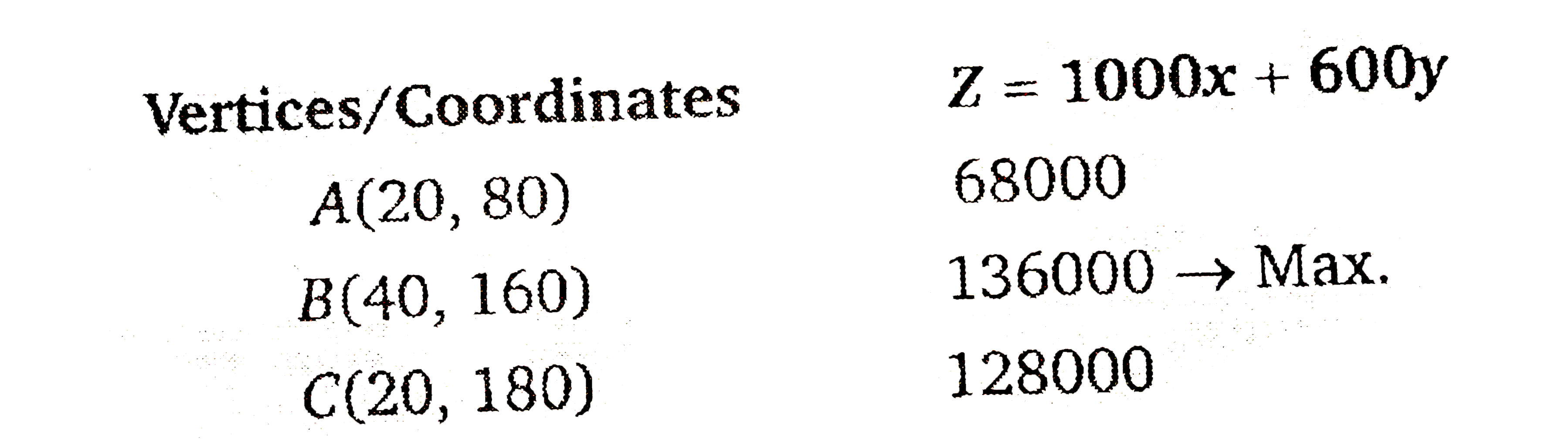
Thus, the maximum value of Z is 136000 at point B(40,160). Therefore, maximum cost is Rs. 136000 for which 40 tickets of executive class and 160 tickets of economy class are required.
Topper's Solved these Questions
- LINEAR PROGRAMMINGBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - Exercise 12.2
11 Videos
- INVERES TRIGONOMETRIC FUNCTIONSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - INVERES TRIGONOMETRIC FUNCTIONSEXERCISE - Miscellaneous Exercise (prove That )
9 Videos
- MATRICESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - MATRICESEXERCISE - Miscellaneous Exerice
15 Videos
Similar Questions
An aeroplane can carry a maximum of 200 passengers. A profit of Rs. 1000 is made on each executive class ticket and a profit of Rs. 600 is made on each economy class ticket. The airline reserves at least 20 seats for executive class. However, at least 4 times as many passengers prefer to travel by economy class than by the executive class. Determine how many tickets of each type must be sold in order to maximize the profit for the airline. What is the maximum profit?
View SolutionAn aeroplane can carry a maximum of 200 passengers. A profit of Rs. 400 is made on each first class ticket and a profit of Rs. 300 is made on each second class ticket. The airline reserves at least 20 seats for first class. However, at least four times as many passengers prefer to travel by second class then by first class. Determine how many tickets of each type must be sold to maximise profit for the airline. Form an LPP and solve it graphically.
View Solution
Knowledge Check
Boys and girls in a class are writing letters. There are twice as many girls as boys in the class, and each girl writes 3 more letters than each boy. If boys write 24 of the 90 total letters written by the class, how many letters does each boy write?
A3B4C5D8
By selling a computer for Rs. 16875, a profit of Rs. 1875 is made. Find the profit percentage.
View SolutionIf the profit made on a packet of tea is Rs 4 and the cost price of the packet is Rs 20, then how much is the profit percentage?
View SolutionIn a charity show Rs 6496 were collected by selling some tickets. If the price of each ticket was Rs 5034, how many tickets were sold?
View SolutionA cylinder manufacturer makes small and large cylinders from a large piece of cardboard. The large cylinder requires 4 sq. m and small cylinder requires 3 sq. m of cardboard. The manufacturer is required to make at least 3 large cylinder and at least twice as many small cylinder as large cylinders. If 60 sq. m of cardboard is in the stock and profit on the small and large cylinders are Rs. 25 and Rs 35 respectively. How many of each type of cylinders to made to maximize the profit. Also, find the maximum profit.
View SolutionA sports team of 11 students is to be constituted, choosing at least 5 from class XI and at least 5 from class XII. if there are 20 students in each of these classes, in how many ways can the team be constituted. What is the importance of sports in one's life ?
View SolutionHow are polymers classified according to their structure? Give important features of each class. Also give two examples of each class.
View SolutionA company produces two types of good, A and B, that require gold and silver. Each unit of type A requires 3 gm of silver and 1 gm of gold while that of type B requires 1 gm of silver and 2 gm of gold. The company can produce 9 gm of silver and 8 gm of gold. If each unit of type A brings a profit of Rs. 40 and that of type B Rs. 50, find the number of units of each type that the company should produce to maximize the profit. What is the maximum profit?
View Solution
