Maximise Z=3x+4y
Subject to the constraints
x+y≤4,x≥0,y≥0
Draw the graph of equation x+y=4.
Now obtain the feasible region for the inequalities x+y≤4,x≥0,y≥0. The convex region is OAB whose are O(0,0),A(4,0) and B(0,4). Now we will find the value of z=3x+4y at each vertex.
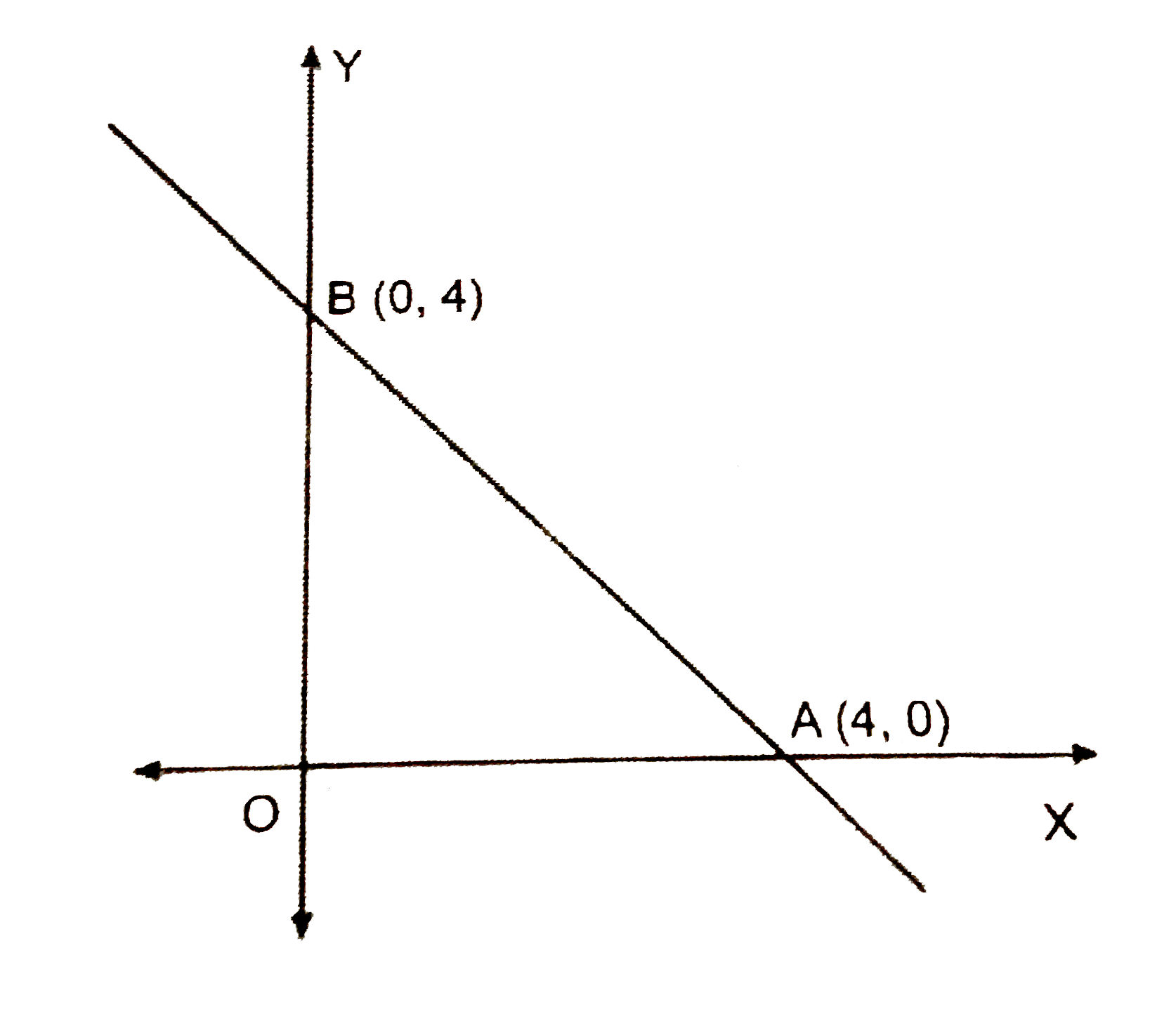
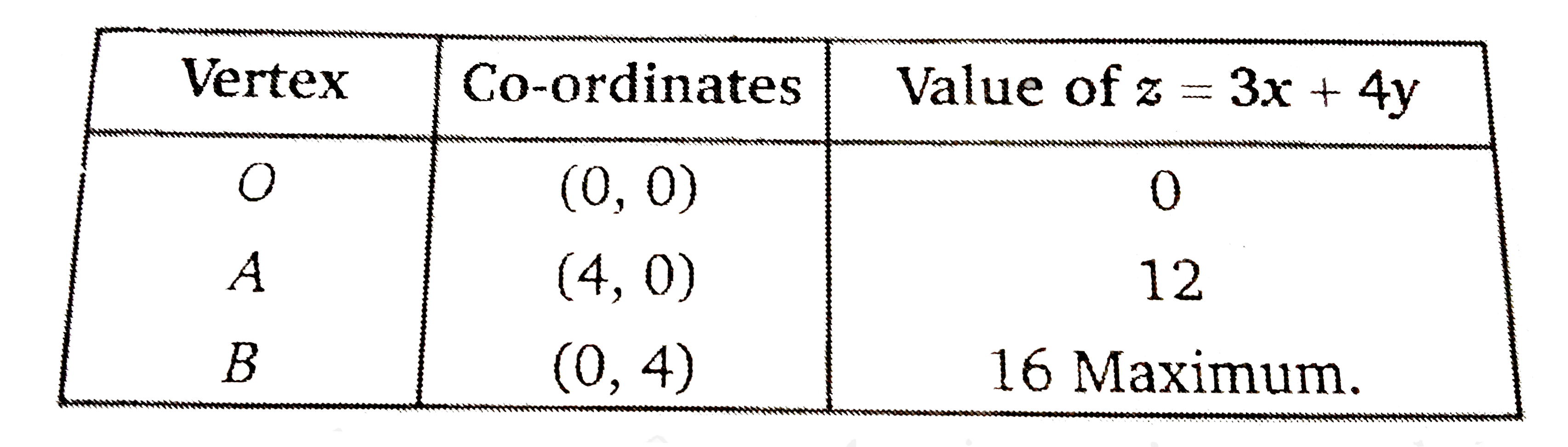
Therefore at x=0,y=4,z is maximum and the maximum value is 16.
Topper's Solved these Questions
- LINEAR PROGRAMMINGBook:NAGEEN PRAKASHAN ENGLISHChapter:LINEAR PROGRAMMINGExercise:Exercise 12 A
Explore 8 Videos
- LINEAR PROGRAMMINGBook:NAGEEN PRAKASHAN ENGLISHChapter:LINEAR PROGRAMMINGExercise:Exercise 12 B
Explore 15 Videos
- INVERES TRIGONOMETRIC FUNCTIONSBook:NAGEEN PRAKASHAN ENGLISHChapter:INVERES TRIGONOMETRIC FUNCTIONSExercise:Miscellaneous Exercise (prove That )
Explore 9 Videos
- MATRICESBook:NAGEEN PRAKASHAN ENGLISHChapter:MATRICESExercise:Miscellaneous Exerice
Explore 15 Videos
Similar Questions
Solve the Following Linear Programming Problem graphically : Maximise Z=3x+4ysubject to the constraints : x+y≤4,x≥0,y≥0.
View SolutionMaximise Z=3x+4y, Subjected to the constraints x+y≤1,x≥0,y≥0
View SolutionMaximise Z=−x+2y
Subject to the constraints x≥3,x+y≥5,x+2y≥6,y≥0
View SolutionSolve the linear programming problem
Maximise Z=x+2y
Subject to the constraints:
x−y≤10,2x+3y≤20 and x≥0,y≥0
View SolutionSolve each of the following linear programming problems by graphical method. Maximize Z=3x+3y Subject to the constraints x−y≤1 x+y≥3 x,y≥0
View SolutionMinimise Z=13x-15y subject to the constraints x+y≤7,2x−3y+6≥0,x≥0,x≥0,andy≥0
View SolutionMaximise the function Z=11x+7y, subject to the constraints x≤3,y≤2,x≥0,y≥0
View SolutionFind the point which provides the solution of linear programming problem:
Maximise: Z=45x + 55y
Subject to constraints: x,y≥0,6x+4y≤120and3x+10y≤180.
View SolutionSolve the following problem graphically:Minimise and Maximise Z=3x+9y . . . (1)subject to the constraints: x+3y≤60 . . . (2) x+y≥10 . . . (3) x≤y . . . (4) x≥0,y≥0 . . . (5)
View SolutionMinimise Z = 6x + 3y, subject to the constraints 4x+y≥80,x+5y≥115,3x+2y≤150,x≥0,y≥0.
View Solution