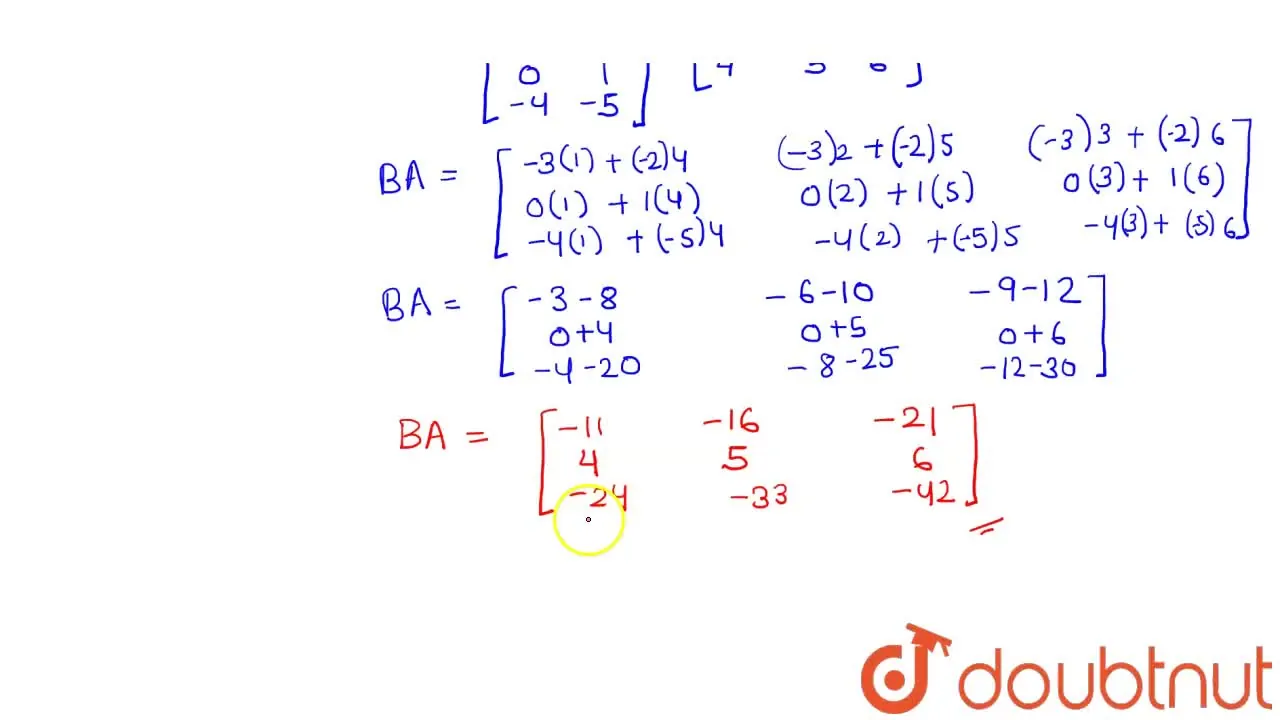
if then find AB and BA ,
Video Solution
Text Solution
The correct Answer is:N/a
No. of columns in A=No . Of rows in B .
AB exists .
Now ,No , of columns in B=N of rows in A.
BA exists.
|
Updated on:21/07/2023
Related Playlists
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - MATRICESEXERCISE - Exercise 3a20videos
MATRICES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - MATRICESEXERCISE - Exercise 3b15videos
MATRICES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - Miscellaneous Exercise9videos
LINEAR PROGRAMMING
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABIILITYEXERCISE - Miscellaneous Exercise19videos
PROBABIILITY
Similar Questions
If A=[2−1345−6]andB=⎡⎢⎣12345−6⎤⎥⎦ then
View SolutionifA=[12−5−346]andB[−23−4123]' then find 2A+B.
View SolutionifA=[40−3120]andB=⎡⎢⎣211−234⎤⎥⎦'then find AB and BA.
View SolutionIf A=[1234]andB=⎡⎢⎣124536⎤⎥⎦, then AB is …………..
View SolutionIf A=⎡⎢⎣123⎤⎥⎦andB=⎡⎢⎣−54002−11−32⎤⎥⎦then AB
View Solutionif 2A+B=[5−132]andA−2B=[1−405] then find the matrices A and B .
View SolutionifA=⎡⎢⎣10−3234−45−2⎤⎥⎦andb=⎡⎢⎣30−125−44−12⎤⎥⎦,then show that :
(AB)'=B'A'View SolutionIf A=[23−1142] and B=⎡⎢⎣234521⎤⎥⎦ then AB and BA are defined and equal.
View Solutionif A=⎡⎢⎣1624−35⎤⎥⎦B=⎡⎢⎣341−22−1⎤⎥⎦, then find a matrix C such that 2A-B+c=0
View SolutionIf A=⎡⎢⎣123−456⎤⎥⎦andB=[4567−82] will AB be equal to BA. Also find AB & BA.
View Solution