Question

Find the direction in which a straight line must be drawn through
the point $(1,2)$
so that its point of
intersection with the line $x+y=4$
may be at a distance of 3
units from this point.

Explanation

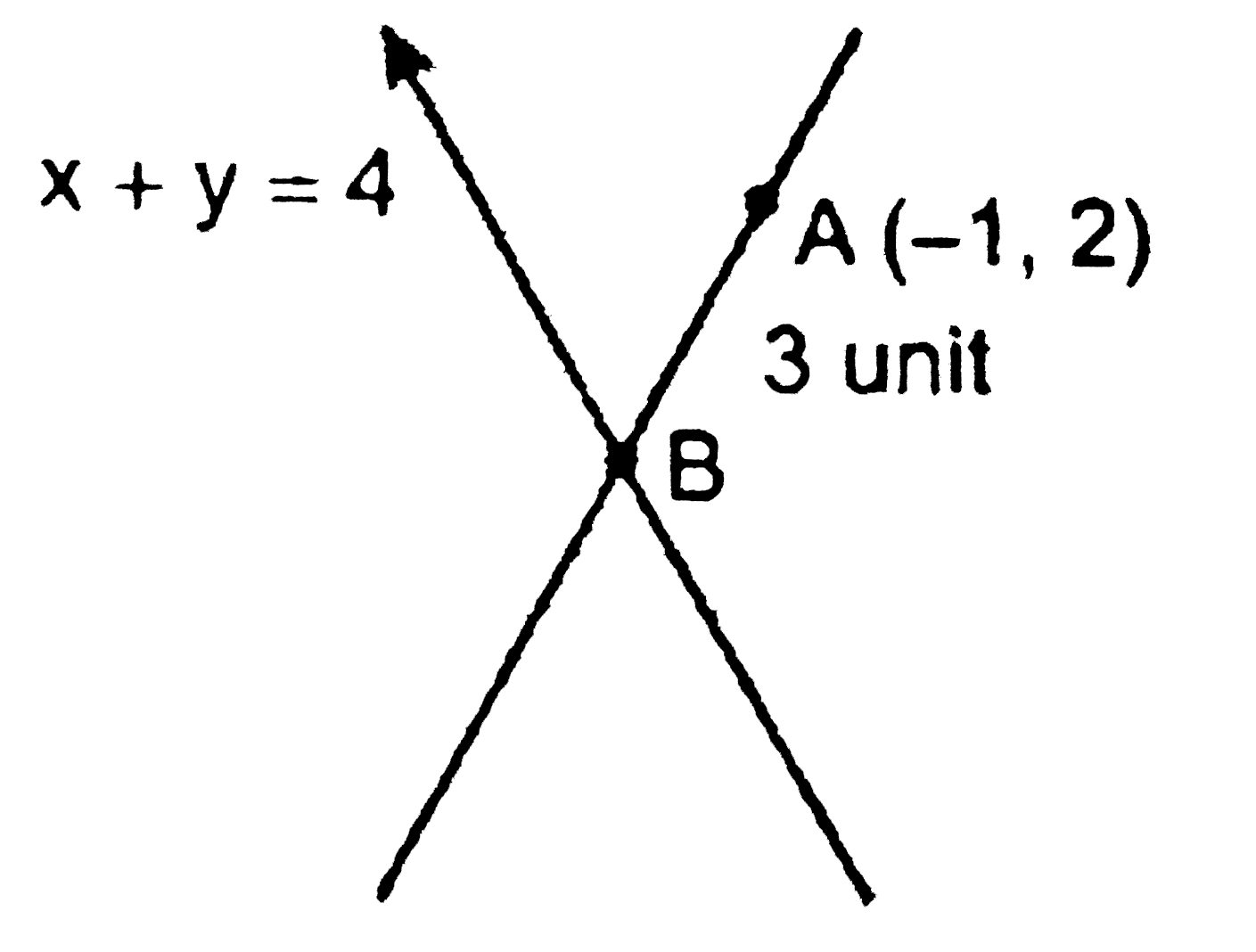
Let the slope of required line passing through the point `(-1,2)` is `m`.
`,.` Equation of line is,
`y-2=m(x+1)`
`impliesmx-y=-2-m`…….`(1)`
Given line is, `x+y=4`……..`(2)`
Solving we get
`x=(2-m)/(m+1)` and `y=(5m+2)/(m+1)`
`:.` Point of intersection is , `B=((2-m)/(m+1),(5m+2)/(m+1))`
Given that `AB=3` units
`impliessqrt(((2-m)/(m+1)+1)^(2)+((5m+2)/(m+1)-2)^(2))=3`
`impliessqrt(((3)^(2)+(3m)^(2))/((m+1)^(2)))=3`
`implies 3^(2)+9m^(2)=9(m+1)^(2)`
`implies 9+9m^(2)=9m^(2)+18m+9`
`implies 4m+18m=0`
`impliesm=0`
Now, `m=0` then `tan theta=0impliestheta=0^(@)`
`implies` Line is parallel to `x`-axis.