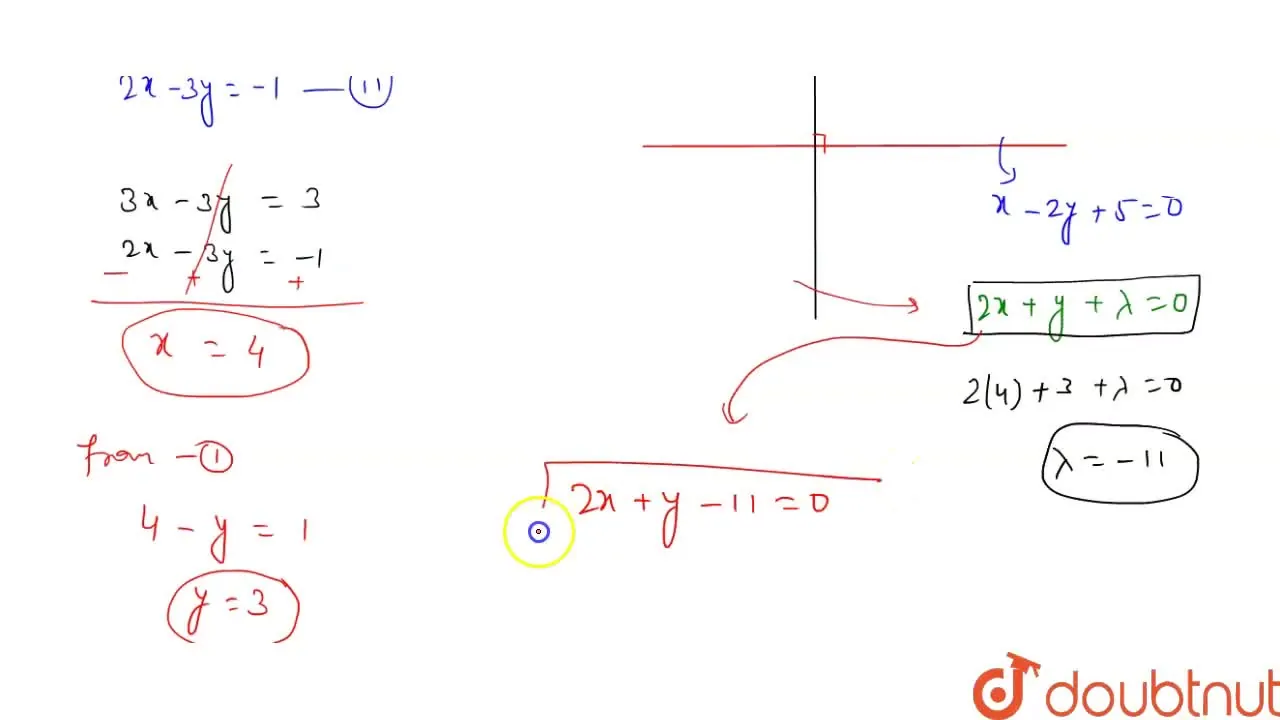
Find the equation of a line passing through the point of intersection of lines x−y−1=0 and 2x−3y+1=0 and perpendicular to the line x−2y+5=0.
Let the equation of a line through the point of intersection of the lines x−y−1=0 and 2x−3y−1=0 be
(x−y−1)+λ(2x−3y+1)=0
⇒x(1+2λ)−y(1+3λ)+(λ−1)=0…..(1)
Its slope is m1=1+2λ1+3λ
Slope of given line x−2y+5=0 is
m2=12
For perpendicular lines
m1m2=−1
1+2λ1+3λ⋅12=−1
⇒1+2λ=−2−6λ
⇒λ=−38
Put in λ=−38 in eq. (1)
x(1−68)−y(1−98)+(−38−1)=0
2x+y−11=0
Related Playlists
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - Exercise207videos
STRAIGHT LINES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - MISCELLANEOUS EXERCISE7videos
STATISTICS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIGNOMETRIC FUNCTIONSEXERCISE - MISCELLANEOUS EXERCISE10videos
TRIGNOMETRIC FUNCTIONS
Similar Questions
Find the equation of a line passing through the point of intersection of the lines 3x+5y=−2 and 5x−2y=7 and perpendicular to the line 4x−5y+1=0.
View SolutionFind the equation of a line passing through the point of intersection of the lines x+3y+1=0 and 2x−y+3=0 and parallel to the line 3x−2y+1=0.
View SolutionFind the equation of the straight line passing through the point of intersection of the lines 5x−6y−1=0 and 3x+2y+5=0 and perpendicular to the line 3x−5y+11=0.
View SolutionFind the equation of the line passing through the point of intersection of the lines x+5y+7=0 and 3x+2y−5=0
(b) perpendicular to the line 7x+2y−5=0View SolutionFind the equation of the line passing through the point of intersection of 7x+6y=71 and 5x−8y=−23 , and perpendicular to the line 4x−2y=1.
View SolutionFind the equation of the straight line drawn through the point of intersection of the lines x+y=4 and 2x−3y=1 and perpendicular to the line cutting off intercepts 5,6 on the axes.
View SolutionFind the equation of the line passing through the point of intersection of the lines x+5y+7=0 and 3x+2y−5=0
(a) parallel to the line 7x+2y−5=0View SolutionFind the equation of the straight line which passes through the point of intersection of lines 3x−4y−7=0and12x−5y−13=0 and is perpendicular to the line 2x−3y+5=0
View SolutionFind the equation of a line passing through the point of intersection of the lines 2x−7y+11=0 and x+3y=8 and passes through the point (2,−3).
View SolutionFind the equation of a straight line passing through the point of intersection of x+2y+3=0 and 3x+4y+7=0 and perpendicular to the straight line x−y+9=0.
View Solution