Find the equation of a line passing through the intersection of the lines 3x+2y=5 and 2x−y=1 and cuts equal intercepts on the axes.
The point of intersection of the lines 3x+2y=5 and 2x−y=1 is (1,1).
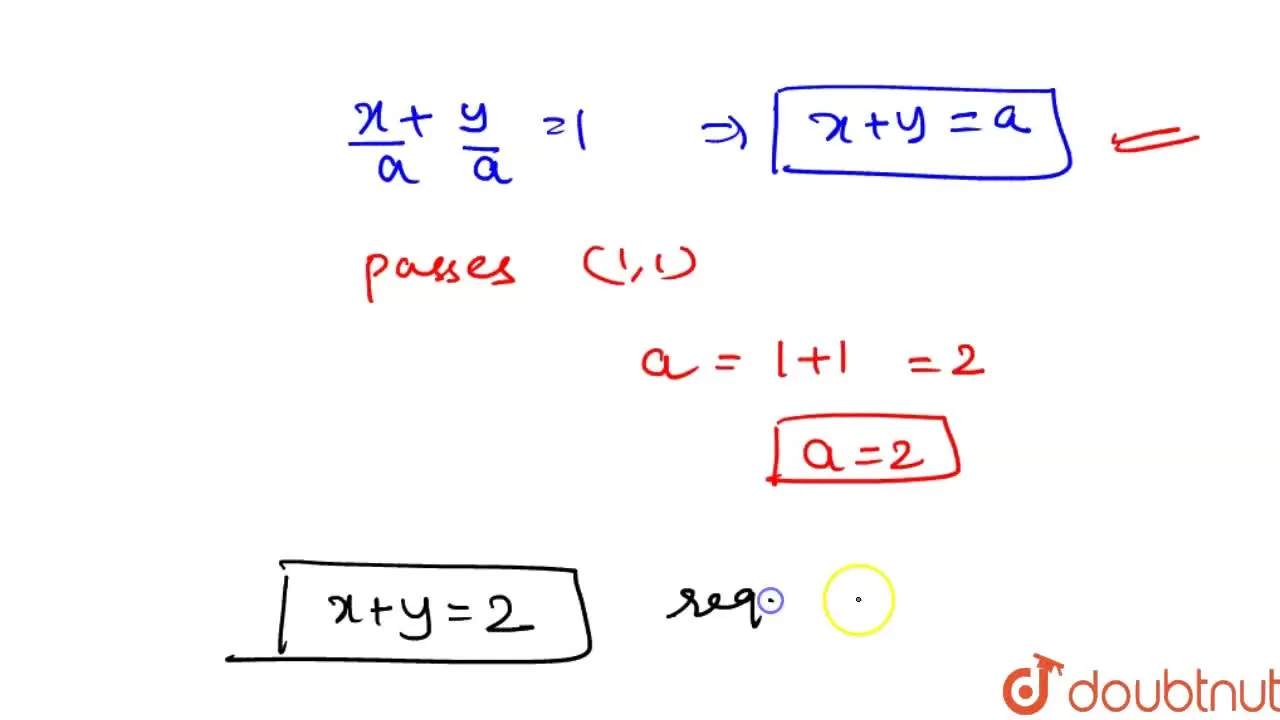
Let the equation of line, cuts equal intercept on axes be
xa+yb=1
⇒x+y=a………(1)
This lines passes through the point (1,1)
1+1=a
⇒a=2
Put a=2 in eq. (1)
x+y=2
Which is required equation of the line.
Related Playlists
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - Exercise207videos
STRAIGHT LINES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - MISCELLANEOUS EXERCISE7videos
STATISTICS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIGNOMETRIC FUNCTIONSEXERCISE - MISCELLANEOUS EXERCISE10videos
TRIGNOMETRIC FUNCTIONS
Similar Questions
Find the equation of the line passing through the intersection of the lines 3x−4y+1=0 and 5x+y−1=0 which cuts off equal intercepts on the axes.
View SolutionFind the equation of a line passing through the intersection of the lines x+3y=4 and 2x−y=1 and (0,0) lies on this line.
View SolutionFind the equation of a line passing through the point of intersection of the lines 5x+y−3=0 and x+3y+1=0 and made equal intercept from the co-ordinates axes.
View SolutionFind the equation of the line passing through the point of intersection of the lines 4x+7y−3=0and 2x−3y+1=0that has equal intercepts on the axes.
View SolutionObtain the equations of the line passing through the intersection of lines 4x−3y−1=0 and 2x−5y+3=0 and equally inclined to the axes.
View SolutionFind the equation of a line passing through the intersection of the lines 3x−y=1 and 5x+2y=9 and parallel to the line 3x+5y=8.
View SolutionFind the equation of the line passing through the point of intersection of the lines 4x−7y−3=0 and 2x−3y+1=0 that has equal intercept to axes.
View SolutionFind the equation of a line passing through the point of intersection of the lines 3x+5y=−2 and 5x−2y=7 and perpendicular to the line 4x−5y+1=0.
View SolutionFind the equation of line through the intersection of lines 3x+4y=7 and x-y+2=0 and whose slope is 5.
View SolutionFind the equation of a line passing through the point of intersection of the lines x+y=4 and 2x−3y−1=0 and parallel to a line whose intercepts on the axes are 4 and 6 units.
View Solution